《2025年学霸题中题九年级数学上册人教版》

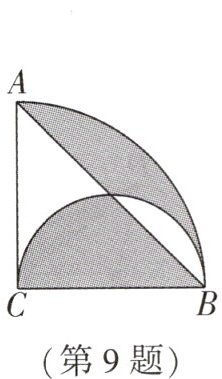
9. (十堰中考)如图,圆心角为$90^{\circ }$的扇形 ACB 内,以 BC 为直径作半圆,连接 AB.若阴影部分的面积为$(\pi - 1)$,则$AC= $2.

答案： 2

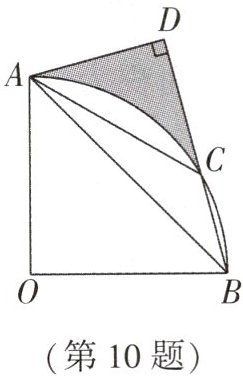
10. (贵港中考)如图,在扇形 OAB 中,点 C 在$\overset{\frown}{AB}$上,$∠AOB= 90^{\circ },∠ABC= 30^{\circ },AD⊥BC$于点 D,连接 AC,若$OA= 2$,则图中阴影部分的面积为______.

答案：
$ 1 + \sqrt{3} - \frac{2}{3}\pi $ 解析: 如图, 连接 $ OC $, 作 $ CM \perp OB $ 于点 $ M $, $ \because \angle AOB = 90^{\circ}, OA = OB = 2 $, $ \therefore \angle ABO = \angle OAB = 45^{\circ}, AB = 2\sqrt{2} $. $ \because \angle ABC = 30^{\circ}, AD \perp BC $ 于 $ D $, $ \therefore AD = \frac{1}{2}AB = \sqrt{2} $, $ \therefore BD = \sqrt{AB^{2} - AD^{2}} = \sqrt{6} $. $ \because \angle ABO = 45^{\circ}, \angle ABC = 30^{\circ} $, $ \therefore \angle OBC = 75^{\circ} $. $ \because OB = OC $, $ \therefore \angle OCB = \angle OBC = 75^{\circ} $, $ \therefore \angle BOC = 30^{\circ} $, $ \therefore \angle AOC = 60^{\circ} $, $ CM = \frac{1}{2}OC = \frac{1}{2} \times 2 = 1 $, $ \therefore S_{\text{阴影}} = S_{\triangle ABD} + S_{\triangle AOB} - S_{\text{扇形}OAC} - S_{\triangle BOC} = \frac{1}{2} \times \sqrt{2} \times \sqrt{6} + \frac{1}{2} \times 2 \times 2 - \frac{60\pi \times 2^{2}}{360} - \frac{1}{2} \times 2 \times 1 = 1 + \sqrt{3} - \frac{2}{3}\pi $.

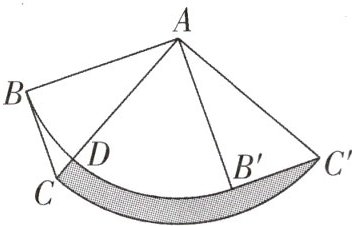
11. (乐山中考)在$\triangle ABC$中,已知$∠ABC= 90^{\circ },∠BAC= 30^{\circ },BC= 1$.如图所示,将$\triangle ABC$绕点 A 按逆时针方向旋转$90^{\circ }后得到\triangle AB'C'$,则图中阴影部分的面积为 (B)

A. $\frac{\pi}{4}$
B. $\frac{\pi - \sqrt{3}}{2}$
C. $\frac{\pi - \sqrt{3}}{4}$
D. $\frac{\sqrt{3}}{2}\pi$

答案： B

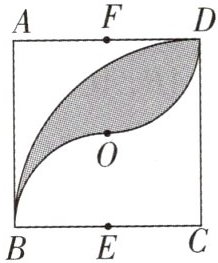
12. (枣庄中考改编)如图,正方形 ABCD 的边长为 2,O 为对角线的交点,点 E,F 分别为 BC,AD 的中点.以 C 为圆心,2 为半径作$\overset{\frown}{BD}$,再分别以 E,F 为圆心,1 为半径作$\overset{\frown}{BO},\overset{\frown}{OD}$,则图中阴影部分的面积为______π - 2.

答案： $ \pi - 2 $

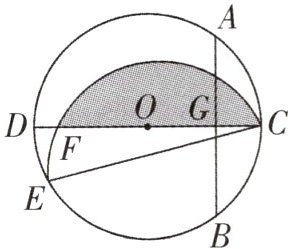
13. 如图,CD 是$\odot O$的直径,AB 是$\odot O$的弦,$AB⊥CD$,垂足为 G,$OG:OC= 3:5,AB= 8$.点 E 为圆上一点,$∠ECD= 15^{\circ }$,将$\overset{\frown}{CE}$沿弦 CE 翻折,交 CD 于点 F,图中阴影部分的面积为______.

答案：
$ \frac{25\pi}{3} - \frac{25\sqrt{3}}{4} $ 解析: 如图, 连接 $ AO $, $ \because CD $ 为 $ \odot O $ 的直径, $ AB \perp CD, AB = 8 $, $ \therefore AG = \frac{1}{2}AB = 4 $. $ \because OG:OC = 3:5 $, $ \therefore $ 设 $ \odot O $ 的半径为 $ 5k $, 则 $ OG = 3k $, $ \therefore (3k)^{2} + 4^{2} = (5k)^{2} $, 解得 $ k = 1 $ 或 $ k = -1 $ (舍去), $ \therefore 5k = 5 $, 即 $ \odot O $ 的半径是 5. 将阴影部分沿 $ CE $ 翻折, 点 $ F $ 的对应点为 $ M $. 连接 $ CM $, $ \because \angle ECD = 15^{\circ} $, $ \therefore $ 由对称性可知, $ \angle DCM = 30^{\circ} $, $ S_{\text{阴影}} = S_{\text{弓形}CBM} $, 连接 $ OM $, 则 $ \angle MOD = 60^{\circ} $, $ \therefore \angle MOC = 120^{\circ} $. 过点 $ M $ 作 $ MN \perp CD $ 于点 $ N $, 由勾股定理得 $ MN = \frac{5\sqrt{3}}{2} $, $ \therefore S_{\text{阴影}} = S_{\text{扇形}OMC} - S_{\triangle OMC} = \frac{120 \times \pi \times 5^{2}}{360} - \frac{1}{2} \times 5 \times \frac{5\sqrt{3}}{2} = \frac{25\pi}{3} - \frac{25\sqrt{3}}{4} $, 即图中阴影部分的面积是 $ \frac{25\pi}{3} - \frac{25\sqrt{3}}{4} $.

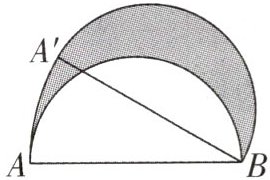
14. (攀枝花中考)如图,直径$AB= 6$的半圆,绕点 B 顺时针旋转$30^{\circ }$,此时点 A 到了点$A'$,则图中阴影部分的面积是 (D)

A. $\frac{\pi}{2}$
B. $\frac{3\pi}{4}$
C. $\pi$
D. $3\pi$

答案： D

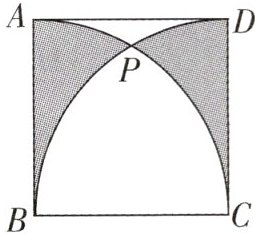
15. (荆门中考)如图,正方形 ABCD 的边长为 2,分别以点 B,C 为圆心,以正方形的边长为半径的圆相交于点 P,那么图中阴影部分的面积为______.

答案：
$ 2\sqrt{3} - \frac{2\pi}{3} $ 解析: 如图, 连接 $ PB, PC $, 作 $ PF \perp BC $ 于点 $ F $, $ \because PB = PC = BC $, $ \therefore \triangle PBC $ 为等边三角形, $ \therefore \angle PBC = 60^{\circ} $, $ \therefore \angle BPF = 30^{\circ} $, $ \therefore BF = \frac{1}{2}PB = 1, PF = \sqrt{3} $, 则图中阴影部分的面积 $ = [ $ 扇形 $ ABP $ 的面积 $ - ( $ 扇形 $ BCP $ 的面积 $ - \triangle BPC $ 的面积 $ ) ] \times 2 = [ \frac{30 \times \pi \times 2^{2}}{360} - ( \frac{60 \times \pi \times 2^{2}}{360} - \frac{1}{2} \times 2 \times \sqrt{3} ) ] \times 2 = 2\sqrt{3} - \frac{2\pi}{3} $.