第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
1. (台州中考)如图①,小球从左侧的斜坡滚下,到达底端后又沿着右侧斜坡向上滚,在这个过程中,小球的运动速度 $ v $ (单位: $ \mathrm{m} / \mathrm{s} $)与运动时间 $ t $ (单位: $ \mathrm{s} $)的函数图象如图②,则该小球的运动路程 $ y $ (单位: $ \mathrm{m} $)与运动时间 $ t $ (单位: $ \mathrm{s} $)之间的函数图象大致是 (

C
)
答案:
C
2. (南通中考)如图,在 $ □ A B C D $ 中,对角线 $ A C $, $ B D $ 相交于点 $ O, A C \perp B C, B C= 4, \angle A B C= 60^{\circ} $,若 $ E F $ 过点 $ O $ 且与边 $ A B, C D $ 分别相交于点 $ E $, $ F $,设 $ B E= x, O E^{2}= y $,则 $ y $ 关于 $ x $ 的函数图象大致为 (
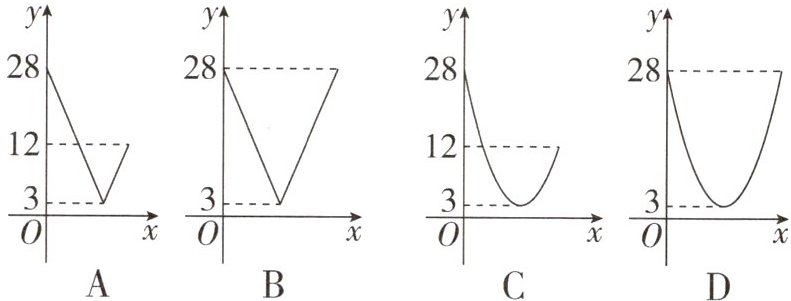

C
)

答案:
C
3. (2023·盘锦中考)如图,在平面直角坐标系中,菱形 $ A B C D $ 的顶点 $ A $ 在 $ y $ 轴的正半轴上,顶点 $ B, C $ 在 $ x $ 轴的正半轴上, $ D(2, \sqrt{3}) $, $ P(-1,-1) $.点 $ M $ 在菱形的边 $ A D $ 和 $ D C $ 上运动(不与点 $ A, C $ 重合),过点 $ M $ 作 $ M N / / y $ 轴,与菱形的另一边交于点 $ N $,连接 $ P M, P N $,设点 $ M $ 的横坐标为 $ x, \triangle P M N $ 的面积为 $ y $,则下列图象能正确反映 $ y $ 与 $ x $ 之间函数关系的是 (


A
)

答案:
A 解析:
∵菱形ABCD的顶点A在y轴的正半轴上,顶点B,C在x轴的正半轴上,
∴AB=AD=2,OA=$\sqrt{3}$,
∴OB=$\sqrt{AB^{2}-OA^{2}}=\sqrt{2^{2}-(\sqrt{3})^{2}}=1$,
∴OC=OB+BC=1+2=3,
∴A(0,$\sqrt{3}$),B(1,0),C(3,0)。设直线AB的解析式为y=kx+b,将A(0,$\sqrt{3}$),B(1,0)代入,得$\begin{cases}k+b=0\\b=\sqrt{3}\end{cases}$,解得$\begin{cases}k=-\sqrt{3}\\b=\sqrt{3}\end{cases}$,
∴直线AB的解析式为y=$-\sqrt{3}$x+$\sqrt{3}$。
∵MN//y轴,
∴点N的横坐标为x。
①当点M的横坐标x在0~1之间时,点N在线段AB上,在△PMN中,MN上的高为1+x,
∴N(x,$-\sqrt{3}$x+$\sqrt{3}$),
∴MN=$\sqrt{3}-(-\sqrt{3}x+\sqrt{3})=\sqrt{3}x$,
∴$S_{\triangle PMN}=\frac{1}{2}MN\cdot(1+x)=\frac{1}{2}\sqrt{3}x\cdot(1+x)=\frac{\sqrt{3}}{2}x^{2}+\frac{\sqrt{3}}{2}x$,
∴该段图象为开口向上的抛物线。
②当点M的横坐标x在1~2之间时,点N在线段BC上,在△PMN中,MN=$\sqrt{3}$,MN上的高为1+x,
∴$S_{\triangle PMN}=\frac{1}{2}MN\cdot(1+x)=\frac{1}{2}\sqrt{3}\cdot(1+x)=\frac{\sqrt{3}}{2}x+\frac{\sqrt{3}}{2}$,
∴该段图象为直线。
③当点M的横坐标x在2~3之间时,点N在线段BC上,在△PMN中,MN上的高为1+x,由D(2,$\sqrt{3}$),C(3,0),可得直线CD的解析式为y=$-\sqrt{3}$x+3$\sqrt{3}$,
∴M(x,$-\sqrt{3}$x+3$\sqrt{3}$),N(x,0),
∴MN=$-\sqrt{3}$x+3$\sqrt{3}$,
∴$S_{\triangle PMN}=\frac{1}{2}MN\cdot(1+x)=\frac{1}{2}(-\sqrt{3}x+3\sqrt{3})\cdot(1+x)=-\frac{\sqrt{3}}{2}x^{2}+\sqrt{3}x+\frac{3\sqrt{3}}{2}$,
∴该段图象为开口向下的抛物线。
观察四个选项可知,只有选项A满足条件。
∵菱形ABCD的顶点A在y轴的正半轴上,顶点B,C在x轴的正半轴上,
∴AB=AD=2,OA=$\sqrt{3}$,
∴OB=$\sqrt{AB^{2}-OA^{2}}=\sqrt{2^{2}-(\sqrt{3})^{2}}=1$,
∴OC=OB+BC=1+2=3,
∴A(0,$\sqrt{3}$),B(1,0),C(3,0)。设直线AB的解析式为y=kx+b,将A(0,$\sqrt{3}$),B(1,0)代入,得$\begin{cases}k+b=0\\b=\sqrt{3}\end{cases}$,解得$\begin{cases}k=-\sqrt{3}\\b=\sqrt{3}\end{cases}$,
∴直线AB的解析式为y=$-\sqrt{3}$x+$\sqrt{3}$。
∵MN//y轴,
∴点N的横坐标为x。
①当点M的横坐标x在0~1之间时,点N在线段AB上,在△PMN中,MN上的高为1+x,
∴N(x,$-\sqrt{3}$x+$\sqrt{3}$),
∴MN=$\sqrt{3}-(-\sqrt{3}x+\sqrt{3})=\sqrt{3}x$,
∴$S_{\triangle PMN}=\frac{1}{2}MN\cdot(1+x)=\frac{1}{2}\sqrt{3}x\cdot(1+x)=\frac{\sqrt{3}}{2}x^{2}+\frac{\sqrt{3}}{2}x$,
∴该段图象为开口向上的抛物线。
②当点M的横坐标x在1~2之间时,点N在线段BC上,在△PMN中,MN=$\sqrt{3}$,MN上的高为1+x,
∴$S_{\triangle PMN}=\frac{1}{2}MN\cdot(1+x)=\frac{1}{2}\sqrt{3}\cdot(1+x)=\frac{\sqrt{3}}{2}x+\frac{\sqrt{3}}{2}$,
∴该段图象为直线。
③当点M的横坐标x在2~3之间时,点N在线段BC上,在△PMN中,MN上的高为1+x,由D(2,$\sqrt{3}$),C(3,0),可得直线CD的解析式为y=$-\sqrt{3}$x+3$\sqrt{3}$,
∴M(x,$-\sqrt{3}$x+3$\sqrt{3}$),N(x,0),
∴MN=$-\sqrt{3}$x+3$\sqrt{3}$,
∴$S_{\triangle PMN}=\frac{1}{2}MN\cdot(1+x)=\frac{1}{2}(-\sqrt{3}x+3\sqrt{3})\cdot(1+x)=-\frac{\sqrt{3}}{2}x^{2}+\sqrt{3}x+\frac{3\sqrt{3}}{2}$,
∴该段图象为开口向下的抛物线。
观察四个选项可知,只有选项A满足条件。
4. (2023·辽宁中考)如图, $ \angle M A N= 60^{\circ} $,在射线 $ A M, A N $ 上分别截取 $ A C= A B= 6 $,连接 $ B C $, $ \angle M A N $ 的平分线交 $ B C $ 于点 $ D $,点 $ E $ 为线段 $ A B $ 上的动点,作 $ E F \perp A M $ 交 $ A M $ 于点 $ F $,作 $ E G / / A M $ 交射线 $ A D $ 于点 $ G $,过点 $ G $ 作 $ G H \perp A M $ 于点 $ H $,点 $ E $ 沿 $ A B $ 方向运动,当点 $ E $ 与点 $ B $ 重合时停止运动.设点 $ E $ 运动的路程为 $ x $,四边形 $ E F H G $ 与 $ \triangle A B C $ 重叠部分的面积为 $ S $,则能大致反映 $ S $ 与 $ x $ 之间函数关系的图象是 ( )




答案:
A 解析:
∵∠MAN=60°,AC=AB=6,
∴△ABC是边长为6的等边三角形。
∵AD平分∠MAN,
∴∠MAD=∠NAD=30°,AD⊥BC,CD=DB=3。
①当矩形EFHG全部在△ABC之中,即由图①到图②,此时0<x≤3,


∵EG//AC,
∴∠MAD=∠AGE=30°,
∴∠NAD=∠AGE=30°,
∴AE=EG=x。在Rt△AEF中,∠EAF=60°,
∴EF=$\frac{\sqrt{3}}{2}AE=\frac{\sqrt{3}}{2}x$,
∴S=$\frac{\sqrt{3}}{2}x^{2}$。
②如图③,当AE+AF=GE+AF=AF+CF=AC时,x+$\frac{1}{2}x=6$,解得x=4,由图②到图③,此时3<x≤4,


如图④,记BC,EG的交点为Q,则△EQB是等边三角形,
∴EQ=EB=BQ=6-x,
∴GQ=x-(6-x)=2x-6,而∠PQG=60°,
∴PG=$\sqrt{3}QG=\sqrt{3}(2x-6)$,
∴S=$S_{矩形EFHG}-S_{\triangle PQG}=\frac{\sqrt{3}}{2}x^{2}-\frac{1}{2}\times(2x-6)\times\sqrt{3}(2x-6)=-\frac{3\sqrt{3}}{2}x^{2}+12\sqrt{3}x-18\sqrt{3}$。
③如图⑥,x=6,即由图③到图⑥,此时4<x≤6,


如图⑤,同理△EKB是等边三角形,
∴EK=KB=EB=6-x,FC=AC-AF=6-$\frac{1}{2}x$,EF=$\frac{\sqrt{3}}{2}x$,
∴S=$S_{梯形EKCF}=\frac{1}{2}(6-x+6-\frac{1}{2}x)\times\frac{\sqrt{3}}{2}x=-\frac{3\sqrt{3}}{8}x^{2}+3\sqrt{3}x$。因此三段函数都是二次函数,其中第1段是开口向上,第2段、第3段是开口向下的抛物线。
A 解析:
∵∠MAN=60°,AC=AB=6,
∴△ABC是边长为6的等边三角形。
∵AD平分∠MAN,
∴∠MAD=∠NAD=30°,AD⊥BC,CD=DB=3。
①当矩形EFHG全部在△ABC之中,即由图①到图②,此时0<x≤3,


∵EG//AC,
∴∠MAD=∠AGE=30°,
∴∠NAD=∠AGE=30°,
∴AE=EG=x。在Rt△AEF中,∠EAF=60°,
∴EF=$\frac{\sqrt{3}}{2}AE=\frac{\sqrt{3}}{2}x$,
∴S=$\frac{\sqrt{3}}{2}x^{2}$。
②如图③,当AE+AF=GE+AF=AF+CF=AC时,x+$\frac{1}{2}x=6$,解得x=4,由图②到图③,此时3<x≤4,


如图④,记BC,EG的交点为Q,则△EQB是等边三角形,
∴EQ=EB=BQ=6-x,
∴GQ=x-(6-x)=2x-6,而∠PQG=60°,
∴PG=$\sqrt{3}QG=\sqrt{3}(2x-6)$,
∴S=$S_{矩形EFHG}-S_{\triangle PQG}=\frac{\sqrt{3}}{2}x^{2}-\frac{1}{2}\times(2x-6)\times\sqrt{3}(2x-6)=-\frac{3\sqrt{3}}{2}x^{2}+12\sqrt{3}x-18\sqrt{3}$。
③如图⑥,x=6,即由图③到图⑥,此时4<x≤6,


如图⑤,同理△EKB是等边三角形,
∴EK=KB=EB=6-x,FC=AC-AF=6-$\frac{1}{2}x$,EF=$\frac{\sqrt{3}}{2}x$,
∴S=$S_{梯形EKCF}=\frac{1}{2}(6-x+6-\frac{1}{2}x)\times\frac{\sqrt{3}}{2}x=-\frac{3\sqrt{3}}{8}x^{2}+3\sqrt{3}x$。因此三段函数都是二次函数,其中第1段是开口向上,第2段、第3段是开口向下的抛物线。
5. (2024·信阳模拟)如图①,已知 $ □ A B C D $ 的边长 $ A B= 4 \sqrt{3}, \angle B= 30^{\circ}, A E \perp B C $ 于点 $ E $.现将 $ \triangle A B E $ 沿 $ B C $ 方向以每秒 1 个单位的速度匀速运动,运动的 $ \triangle A B E $ 与 $ □ A B C D $ 重叠部分的面积 $ S $ 与运动时间 $ t $ 的函数图象如图②,则当 $ t $ 为 9 时, $ S $ 的值是 (
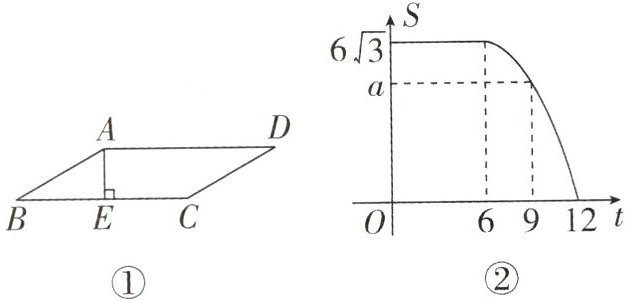
A. $ \frac{8 \sqrt{3}}{3} $
B. $ 3 \sqrt{3} $
C. $ \frac{9 \sqrt{3}}{2} $
D. $ 5 \sqrt{3} $
C
)
A. $ \frac{8 \sqrt{3}}{3} $
B. $ 3 \sqrt{3} $
C. $ \frac{9 \sqrt{3}}{2} $
D. $ 5 \sqrt{3} $
答案:
C 解析:
∵AB=4$\sqrt{3}$,∠B=30°,AE⊥BC于点E,
∴AE=2$\sqrt{3}$,
∴BE=$\sqrt{AB^{2}-AE^{2}}=6$。由运动的△ABE与▱ABCD重叠部分的面积S与运动时间t的函数图象得,当运动时间t≤6时,重叠部分的面积一直不变,
∴CE=6,
∴BC=12;当t>6时,为二次函数图象,且在t=6时达到最大值,对称轴为直线t=6,二次函数图象与坐标轴的另一个交点为(0,0),设二次函数的解析式为S=at(t-12),将点(6,6$\sqrt{3}$)代入得a=$-\frac{\sqrt{3}}{6}$,
∴S=$-\frac{\sqrt{3}}{6}t(t-12)$,当t=9时,S=$\frac{9\sqrt{3}}{2}$。故选C。
∵AB=4$\sqrt{3}$,∠B=30°,AE⊥BC于点E,
∴AE=2$\sqrt{3}$,
∴BE=$\sqrt{AB^{2}-AE^{2}}=6$。由运动的△ABE与▱ABCD重叠部分的面积S与运动时间t的函数图象得,当运动时间t≤6时,重叠部分的面积一直不变,
∴CE=6,
∴BC=12;当t>6时,为二次函数图象,且在t=6时达到最大值,对称轴为直线t=6,二次函数图象与坐标轴的另一个交点为(0,0),设二次函数的解析式为S=at(t-12),将点(6,6$\sqrt{3}$)代入得a=$-\frac{\sqrt{3}}{6}$,
∴S=$-\frac{\sqrt{3}}{6}t(t-12)$,当t=9时,S=$\frac{9\sqrt{3}}{2}$。故选C。
查看更多完整答案,请扫码查看


