第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
12. (金华中考)在一空旷场地上设计一落地为矩形ABCD的小屋,AB + BC = 10 m,拴住小狗的10 m长的绳子一端固定在点B处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为$S(m^2).$
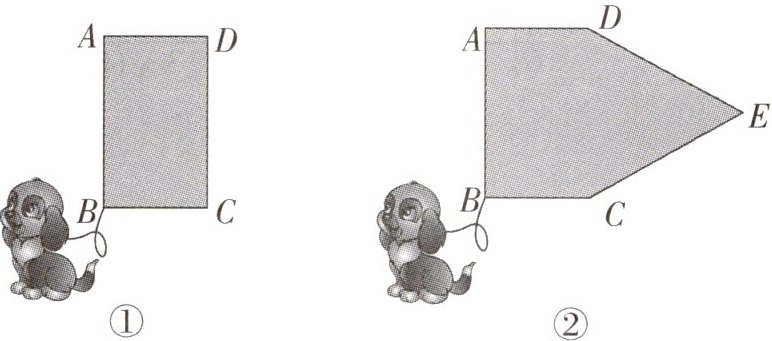
(1)如图①,若BC = 4 m,则$S = ______m^2;$
(2)如图②,现考虑在图①中的矩形ABCD小屋的右侧以CD为边拓展一等边△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,则在BC的变化过程中,当S取得最小值时,边BC的长为______m.

(1)如图①,若BC = 4 m,则$S = ______m^2;$
(2)如图②,现考虑在图①中的矩形ABCD小屋的右侧以CD为边拓展一等边△CDE区域,使之变成落地为五边形ABCED的小屋,其他条件不变,则在BC的变化过程中,当S取得最小值时,边BC的长为______m.
答案:
(1) 88π
(2) $\frac{5}{2}$
解析:
(1) 拴住小狗的10 m长的绳子一端固定在点B处,小狗可以活动的区域如图①所示。由图可知,小狗活动的区域面积为以B为圆心,10 m为半径的$\frac{3}{4}$圆,以C为圆心,6 m为半径的$\frac{1}{4}$圆和以A为圆心,4 m为半径的$\frac{1}{4}$圆的面积和,
∴S = $\frac{3}{4}\pi \cdot 10^{2} + \frac{1}{4}\pi \cdot 6^{2} + \frac{1}{4}\pi \cdot 4^{2} = 88\pi(m^{2})$。
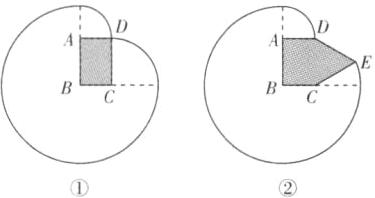
(2) 如图②,设BC = x m,则AB = (10 - x) m,
∴S = $\frac{3}{4}\pi \cdot 10^{2} + \frac{1}{4}\pi \cdot x^{2} + \frac{30}{360} \cdot \pi \cdot (10 - x)^{2} = \frac{\pi}{3}(x^{2} - 5x + 250) = \frac{\pi}{3}(x - \frac{5}{2})^{2} + \frac{325\pi}{4}$,当x = $\frac{5}{2}$时,S取得最小值,即BC = $\frac{5}{2}$ m时,S取得最小值。
(1) 88π
(2) $\frac{5}{2}$
解析:
(1) 拴住小狗的10 m长的绳子一端固定在点B处,小狗可以活动的区域如图①所示。由图可知,小狗活动的区域面积为以B为圆心,10 m为半径的$\frac{3}{4}$圆,以C为圆心,6 m为半径的$\frac{1}{4}$圆和以A为圆心,4 m为半径的$\frac{1}{4}$圆的面积和,
∴S = $\frac{3}{4}\pi \cdot 10^{2} + \frac{1}{4}\pi \cdot 6^{2} + \frac{1}{4}\pi \cdot 4^{2} = 88\pi(m^{2})$。

(2) 如图②,设BC = x m,则AB = (10 - x) m,
∴S = $\frac{3}{4}\pi \cdot 10^{2} + \frac{1}{4}\pi \cdot x^{2} + \frac{30}{360} \cdot \pi \cdot (10 - x)^{2} = \frac{\pi}{3}(x^{2} - 5x + 250) = \frac{\pi}{3}(x - \frac{5}{2})^{2} + \frac{325\pi}{4}$,当x = $\frac{5}{2}$时,S取得最小值,即BC = $\frac{5}{2}$ m时,S取得最小值。
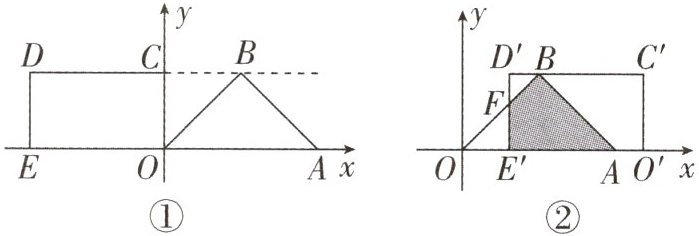
13. (天津中考)在平面直角坐标系中,O为原点,△OAB是等腰直角三角形,∠OBA = 90°,BO = BA,顶点A(4,0),点B在第一象限,矩形OCDE的顶点E(-$\frac{7}{2}$,0),点C在y轴的正半轴上,点D在第二象限,射线DC经过点B.
(1)如图①,求点B的坐标.
(2)将矩形OCDE沿x轴向右平移,得到矩形O'C'D'E',点O,C,D,E的对应点分别为O',C',D',E'.设OO' = t,矩形O'C'D'E'与△OAB重叠部分的面积为S.
①如图②,当点E'在x轴正半轴上,且矩形O'C'D'E'与△OAB重叠部分为四边形时,D'E'与OB相交于点F,试用含有t的式子表示S,并直接写出t的取值范围;
②当$\frac{5}{2}$ ≤ t ≤ $\frac{9}{2}$时,求S的取值范围.
(1)如图①,求点B的坐标.
(2)将矩形OCDE沿x轴向右平移,得到矩形O'C'D'E',点O,C,D,E的对应点分别为O',C',D',E'.设OO' = t,矩形O'C'D'E'与△OAB重叠部分的面积为S.
①如图②,当点E'在x轴正半轴上,且矩形O'C'D'E'与△OAB重叠部分为四边形时,D'E'与OB相交于点F,试用含有t的式子表示S,并直接写出t的取值范围;
②当$\frac{5}{2}$ ≤ t ≤ $\frac{9}{2}$时,求S的取值范围.

答案:
(1) 如图①,过点B作BH⊥OA,垂足为H,由点A(4, 0),得OA = 4,
∵BO = BA,∠OBA = 90°,
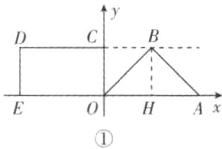
∴OH = BH = $\frac{1}{2}$OA = $\frac{1}{2} \times 4 = 2$,
∴点B的坐标为(2, 2)。
(2) ① 由点E(-$\frac{7}{2}$, 0),得OE = $\frac{7}{2}$,由平移知,四边形O'C'D'E'是矩形,得∠O'E'D' = 90°,O'E' = OE = $\frac{7}{2}$,
∴OE' = OO' - O'E' = t - $\frac{7}{2}$,∠FE'O = 90°。
∵BO = BA,∠OBA = 90°,
∴∠BOA = ∠BAO = 45°,
∴∠OFE' = 90° - ∠BOA = 45°,
∴∠FOE' = ∠OFE',
∴FE' = OE' = t - $\frac{7}{2}$,
∴S△FOE' = $\frac{1}{2}$OE'·FE' = $\frac{1}{2}(t - \frac{7}{2})^{2}$,
∴S = S△OAB - S△FOE' = $\frac{1}{2} \times 4 \times 2 - \frac{1}{2}(t - \frac{7}{2})^{2}$,即S = -$\frac{1}{2}$t² + $\frac{7}{2}$t - $\frac{17}{8}$(4 ≤ t < $\frac{11}{2}$)。
② 当4 < t ≤ $\frac{9}{2}$时,由①知S = -$\frac{1}{2}$t² + $\frac{7}{2}$t - $\frac{17}{8} = -\frac{1}{2}(t - \frac{7}{2})^{2} + 4$,
∴当t = 4时,S有最大值为$\frac{31}{8}$,当t = $\frac{9}{2}$时,S有最小值为$\frac{7}{2}$,
∴此时$\frac{7}{2} \leq S < \frac{31}{8}$;
当$\frac{7}{2} < t \leq 4$时,如图②,令O'C'与AB交于点M,D'E'与OB交于点N,
∴S = S△OAB - S△OE'N - S△O'AM = 4 - $\frac{1}{2}(t - \frac{7}{2})^{2} - \frac{1}{2}(4 - t)^{2} = -t^{2} + \frac{15}{2}t - \frac{81}{8} = -(t - \frac{15}{4})^{2} + \frac{63}{16}$,此时,当t = $\frac{15}{4}$时,S有最大值为$\frac{63}{16}$,当t = 4时,S有最小值为$\frac{31}{8}$,
∴$\frac{31}{8} \leq S \leq \frac{63}{16}$;
当$\frac{5}{2} \leq t \leq \frac{7}{2}$时,如图③,令O'C'与AB交于点M',此时点D'位于第二象限,
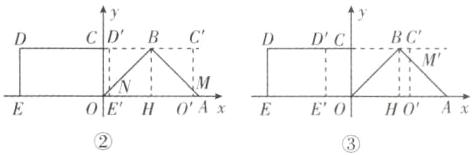
∴S = S△OAB - S△O'AM' = 4 - $\frac{1}{2}(4 - t)^{2} = -\frac{1}{2}(t - 4)^{2} + 4$,此时,当t = $\frac{5}{2}$时,S有最小值为$\frac{23}{8}$,当t = $\frac{7}{2}$时,S有最大值为$\frac{31}{8}$,
∴$\frac{23}{8} \leq S \leq \frac{31}{8}$。
综上,S的取值范围为$\frac{23}{8} \leq S \leq \frac{63}{16}$。
(1) 如图①,过点B作BH⊥OA,垂足为H,由点A(4, 0),得OA = 4,
∵BO = BA,∠OBA = 90°,

∴OH = BH = $\frac{1}{2}$OA = $\frac{1}{2} \times 4 = 2$,
∴点B的坐标为(2, 2)。
(2) ① 由点E(-$\frac{7}{2}$, 0),得OE = $\frac{7}{2}$,由平移知,四边形O'C'D'E'是矩形,得∠O'E'D' = 90°,O'E' = OE = $\frac{7}{2}$,
∴OE' = OO' - O'E' = t - $\frac{7}{2}$,∠FE'O = 90°。
∵BO = BA,∠OBA = 90°,
∴∠BOA = ∠BAO = 45°,
∴∠OFE' = 90° - ∠BOA = 45°,
∴∠FOE' = ∠OFE',
∴FE' = OE' = t - $\frac{7}{2}$,
∴S△FOE' = $\frac{1}{2}$OE'·FE' = $\frac{1}{2}(t - \frac{7}{2})^{2}$,
∴S = S△OAB - S△FOE' = $\frac{1}{2} \times 4 \times 2 - \frac{1}{2}(t - \frac{7}{2})^{2}$,即S = -$\frac{1}{2}$t² + $\frac{7}{2}$t - $\frac{17}{8}$(4 ≤ t < $\frac{11}{2}$)。
② 当4 < t ≤ $\frac{9}{2}$时,由①知S = -$\frac{1}{2}$t² + $\frac{7}{2}$t - $\frac{17}{8} = -\frac{1}{2}(t - \frac{7}{2})^{2} + 4$,
∴当t = 4时,S有最大值为$\frac{31}{8}$,当t = $\frac{9}{2}$时,S有最小值为$\frac{7}{2}$,
∴此时$\frac{7}{2} \leq S < \frac{31}{8}$;
当$\frac{7}{2} < t \leq 4$时,如图②,令O'C'与AB交于点M,D'E'与OB交于点N,
∴S = S△OAB - S△OE'N - S△O'AM = 4 - $\frac{1}{2}(t - \frac{7}{2})^{2} - \frac{1}{2}(4 - t)^{2} = -t^{2} + \frac{15}{2}t - \frac{81}{8} = -(t - \frac{15}{4})^{2} + \frac{63}{16}$,此时,当t = $\frac{15}{4}$时,S有最大值为$\frac{63}{16}$,当t = 4时,S有最小值为$\frac{31}{8}$,
∴$\frac{31}{8} \leq S \leq \frac{63}{16}$;
当$\frac{5}{2} \leq t \leq \frac{7}{2}$时,如图③,令O'C'与AB交于点M',此时点D'位于第二象限,

∴S = S△OAB - S△O'AM' = 4 - $\frac{1}{2}(4 - t)^{2} = -\frac{1}{2}(t - 4)^{2} + 4$,此时,当t = $\frac{5}{2}$时,S有最小值为$\frac{23}{8}$,当t = $\frac{7}{2}$时,S有最大值为$\frac{31}{8}$,
∴$\frac{23}{8} \leq S \leq \frac{31}{8}$。
综上,S的取值范围为$\frac{23}{8} \leq S \leq \frac{63}{16}$。
查看更多完整答案,请扫码查看


