《2025年学霸题中题九年级数学上册人教版》

1. (2023·襄阳中考)我国南宋数学家杨辉在1275年提出的一个问题:“直田积八百六十四步,只云阔不及长一十二步.问阔及长各几步.”意思是:长方形的面积是864平方步,宽比长少12步,问宽和长各是几步.设宽为x步,根据题意列方程正确的是 (D)
A. $ 2x + 2(x + 12) = 864 $
B. $ x^{2} + (x + 12)^{2} = 864 $
C. $ x(x - 12) = 864 $
D. $ x(x + 12) = 864 $

答案： D

2. 教材P20探究3变式 在一幅长为50 cm,宽为30 cm的矩形风景画的四周镶一条相同宽度的金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是1800 $ \mathrm{cm}^{2} $,设金色纸边的宽为x cm,则x满足的方程是 (B)

A. $ x^{2} + 80x - 300 = 0 $
B. $ x^{2} + 40x - 75 = 0 $
C. $ x^{2} - 80x - 300 = 0 $
D. $ x^{2} - 40x - 75 = 0 $

答案： B

3. (沈阳中考改编)某校团体操表演队伍有6行8列,后又增加了51人,使得团体操表演队伍增加的行、列数相同,设增加了x行,则可列方程为(6+x)(8+x)=6×8+51.

答案： $(6+x)(8+x)=6×8+51$

4. (2023·无锡中考)《九章算术》中提出了如下问题:今有户不知高、广,竿不知长、短,横之不出四尺,从之不出二尺,邪之适出,问户高、广、邪各几何? 这段话的意思是:今有门不知其高宽,有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽和对角线的长各是多少? 则该问题中的门高是8尺.

答案： 8

5. 教材P22习题T9变式 现要在一个长为40 m,宽为26 m的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为864 $ \mathrm{m}^{2} $,那么小道的宽度应是2m.

答案： 2

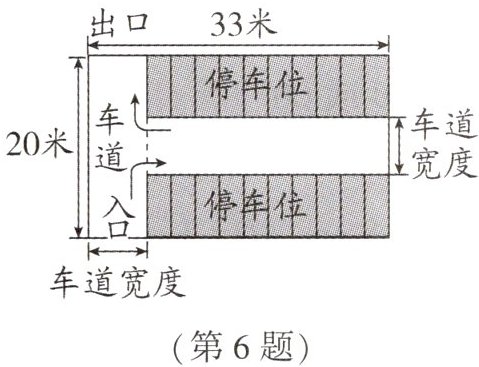
6. 如图是某停车场的平面示意图,停车场外围的长为33米,宽为20米.停车场内车道的宽都相等.若停车位的总占地面积为510平方米,则车道的宽度为3米.

答案： 3

7. 教材P25复习题T8变式 (2023·东营中考)如图,老李想用长为70 m的栅栏,再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD,并在边BC上留一个2 m宽的门(建在EF处,另用其他材料).
(1)当羊圈的长和宽分别为多少米时,能围成一个面积为640 $\mathrm{m}^{2} $的羊圈?
答：当羊圈的长为40m，宽为16m或长为32m，宽为20m时，能围成一个面积为$640m^{2}$的羊圈。
(2)羊圈的面积能达到650 $\mathrm{m}^{2} $吗? 如果能,请你给出设计方案;如果不能,请说明理由.
答：不能，理由：由题意，得$x(72 - 2x) = 650$，化简得$x^{2} - 36x + 325 = 0$，$\Delta = (-36)^{2} - 4×325 = -4 ＜ 0$，∴ 一元二次方程没有实数根。∴ 羊圈的面积不能达到$650m^{2}$。

答案：
(1) 设矩形 $ABCD$ 的边 $AB = x$ m，则边 $BC = 70 - 2x + 2 = (72 - 2x)$ m。根据题意得 $x(72 - 2x) = 640$，化简得 $x^{2} - 36x + 320 = 0$，解得 $x_{1} = 16$，$x_{2} = 20$，当 $x = 16$ 时，$72 - 2x = 72 - 32 = 40$ (m)，当 $x = 20$ 时，$72 - 2x = 72 - 40 = 32$ (m)。答：当羊圈的长为 40 m，宽为 16 m 或长为 32 m，宽为 20 m 时，能围成一个面积为 $640m^{2}$ 的羊圈。
(2) 不能，理由：由题意，得 $x(72 - 2x) = 650$，化简得 $x^{2} - 36x + 325 = 0$，$\Delta = (-36)^{2} - 4×325 = -4 ＜ 0$，
∴ 一元二次方程没有实数根。
∴ 羊圈的面积不能达到 $650m^{2}$。
归纳总结
实际应用之面积问题
$\begin{cases}边框问题\begin{cases}长宽比相等\\四周宽相等\end{cases}\\甬道问题\begin{cases}可平移的甬道\\不可平移的甬道\end{cases}\\围栏问题\begin{cases}围三边：有门、无门\\围四边：有门、无门\end{cases}\end{cases}$