第125页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
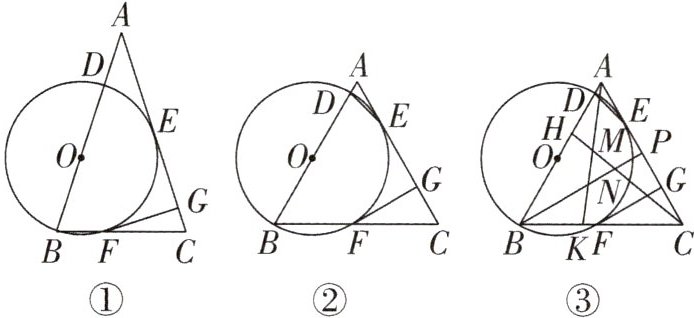
1. 已知:在$\triangle ABC$中,$AB = AC$,点D是AB上一点,以BD为直径的$\odot O$与AC边相切于点E,交BC于点F,$FG\perp AC$于点G.
(1)如图①,求证:$GE = GF$;
(2)如图②,连接DE,$\angle GFC = 2\angle AED$,求证:$\triangle ABC$为等边三角形;
(3)如图③,在(2)的条件下,点H,K,P分别在AB,BC,AC上,AK,BP分别交CH于点M,N,$AH = BK$,$\angle PNC - \frac{1}{2}\angle BAK = 60^{\circ}$,$CN = 6$,$CM = 4\sqrt{3}$,求BC的长.
(1)如图①,求证:$GE = GF$;
(2)如图②,连接DE,$\angle GFC = 2\angle AED$,求证:$\triangle ABC$为等边三角形;
(3)如图③,在(2)的条件下,点H,K,P分别在AB,BC,AC上,AK,BP分别交CH于点M,N,$AH = BK$,$\angle PNC - \frac{1}{2}\angle BAK = 60^{\circ}$,$CN = 6$,$CM = 4\sqrt{3}$,求BC的长.

答案:
(1)如图①,连接OE和OF,
∵AC是⊙O的切线,
∴OE⊥AC,
∴∠OEG=90°.
∵FG⊥AC,
∴∠FGE=90°.
∵AB=AC,
∴∠ABC=∠ACB.
∵OB=OF,
∴∠OBF=∠OFB,
∴∠OBF=∠ACB,
∴OF//AC,
∴∠OFG+∠FGE=180°,
∴∠OFG=90°,
∴∠OFG=∠FGE=∠OEG=90°,
∴四边形OFGE为矩形.
∵OF=OE,
∴四边形OFGE为正方形,
∴GE=GF.

(2)如图②,连接OE,BE,
∵BD是⊙O的直径,
∴∠BED=90°,
∴∠OED+∠OEB=90°.
∵∠OEA=90°,
∴∠AED+∠OED=90°,
∴∠OEB=∠AED.
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OBE=∠AED,
∴∠AOE=2∠OEB=2∠AED.
∵∠GFC=2∠AED,
∴∠AOE=∠GFC.
∵∠C+∠GFC=90°,∠A+∠AOE=90°,
∴∠C=∠A,
∴BA=BC.
∵AB=AC,
∴AB=AC=BC,
∴△ABC为等边三角形.
(3)
∵△ABC为等边三角形,
∴∠CAH=∠ABK=60°.
∵AH=BK,AC=AB,
∴△CAH≌△ABK(SAS),
∴∠ACH=∠BAK.
∵∠KMC=∠KAC+∠ACM,
∴∠KMC=∠KAC+∠BAK=60°.如图③,过点C作CQ⊥AK,垂足为Q,过点B作BT⊥CH,垂足为T,
∴∠AQC=∠CTB=90°.
∵∠QAC=∠BAC−∠BAK=60°−∠BAK,∠TCB=∠ACB−∠ACH=60°−∠ACH,
∴∠QAC=∠TCB.
∵AC=BC,
∴△AQC≌△CTB(AAS),
∴QC=BT.在Rt△MQC中,
∵CM=4√3,∠QMC=60°,∠QCM=30°,
∴QM=1/2CM=2√3,
∴QC=6.设∠BAK=2α=∠ACH.
∵∠PNC−1/2∠BAK=60°,
∴∠PNC=60°+α=∠BNH.
∴∠BCH=∠ACB−∠ACH=60°−2α.延长NH到点R,使RT=TN,连接BR,
∴BT是RN的垂直平分线,
∴BR=BN,
∴∠BNR=∠BRN=60°+α,
∴∠CBR=180°−∠BCR−∠CRB=60°+α,
∴∠CBR=∠CRB=60°+α,
∴BC=RC.设TN=RT=a,
∵CN=6,
∴CT=a+6,CR=CB=2a+6.
∵CQ=BT=6,在Rt△BTC中,BT²+TC²=BC²,
∴6²+(a+6)²=(2a+6)²,
∴a₁=−6(舍),a₂=2,
∴TN=2,BC=10.
(1)如图①,连接OE和OF,
∵AC是⊙O的切线,
∴OE⊥AC,
∴∠OEG=90°.
∵FG⊥AC,
∴∠FGE=90°.
∵AB=AC,
∴∠ABC=∠ACB.
∵OB=OF,
∴∠OBF=∠OFB,
∴∠OBF=∠ACB,
∴OF//AC,
∴∠OFG+∠FGE=180°,
∴∠OFG=90°,
∴∠OFG=∠FGE=∠OEG=90°,
∴四边形OFGE为矩形.
∵OF=OE,
∴四边形OFGE为正方形,
∴GE=GF.

(2)如图②,连接OE,BE,
∵BD是⊙O的直径,
∴∠BED=90°,
∴∠OED+∠OEB=90°.
∵∠OEA=90°,
∴∠AED+∠OED=90°,
∴∠OEB=∠AED.
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OBE=∠AED,
∴∠AOE=2∠OEB=2∠AED.
∵∠GFC=2∠AED,
∴∠AOE=∠GFC.
∵∠C+∠GFC=90°,∠A+∠AOE=90°,
∴∠C=∠A,
∴BA=BC.
∵AB=AC,
∴AB=AC=BC,
∴△ABC为等边三角形.
(3)
∵△ABC为等边三角形,
∴∠CAH=∠ABK=60°.
∵AH=BK,AC=AB,
∴△CAH≌△ABK(SAS),
∴∠ACH=∠BAK.
∵∠KMC=∠KAC+∠ACM,
∴∠KMC=∠KAC+∠BAK=60°.如图③,过点C作CQ⊥AK,垂足为Q,过点B作BT⊥CH,垂足为T,
∴∠AQC=∠CTB=90°.
∵∠QAC=∠BAC−∠BAK=60°−∠BAK,∠TCB=∠ACB−∠ACH=60°−∠ACH,
∴∠QAC=∠TCB.
∵AC=BC,
∴△AQC≌△CTB(AAS),
∴QC=BT.在Rt△MQC中,
∵CM=4√3,∠QMC=60°,∠QCM=30°,
∴QM=1/2CM=2√3,
∴QC=6.设∠BAK=2α=∠ACH.
∵∠PNC−1/2∠BAK=60°,
∴∠PNC=60°+α=∠BNH.
∴∠BCH=∠ACB−∠ACH=60°−2α.延长NH到点R,使RT=TN,连接BR,
∴BT是RN的垂直平分线,
∴BR=BN,
∴∠BNR=∠BRN=60°+α,
∴∠CBR=180°−∠BCR−∠CRB=60°+α,
∴∠CBR=∠CRB=60°+α,
∴BC=RC.设TN=RT=a,
∵CN=6,
∴CT=a+6,CR=CB=2a+6.
∵CQ=BT=6,在Rt△BTC中,BT²+TC²=BC²,
∴6²+(a+6)²=(2a+6)²,
∴a₁=−6(舍),a₂=2,
∴TN=2,BC=10.
2. (包头中考)如图,在$\odot O$中,B是$\odot O$上的一点,$\angle ABC = 120^{\circ}$,弦$AC = 2\sqrt{3}$,弦BM平分$\angle ABC$交AC于点D,连接MA,MC.
(1)求$\odot O$的半径长;
(2)求证:$AB + BC = BM$.
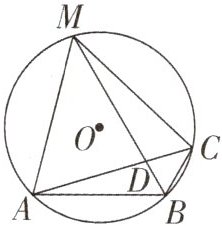
(1)求$\odot O$的半径长;
(2)求证:$AB + BC = BM$.

答案:
(1)连接OA,OC,过O作OH⊥AC于点H,如图①,
∵∠ABC=120°,
∴∠AMC=180°−∠ABC=60°,
∴∠AOC=2∠AMC=120°,
∴∠AOH=1/2∠AOC=60°.
∵AH=1/2AC=√3,∠OAH=30°,
∴OH=1/2AO,
∴由勾股定理得OA=2,故⊙O的半径长为2.


(2)在BM上截取BE=BC,连接CE,如图②,
∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠CBM=60°.
∵BE=BC,
∴△EBC是等边三角形,
∴CE=CB=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°.
∵∠ACM=∠ABM=60°,
∴∠ECM+∠DCE=60°,
∴∠ECM=∠BCD.
∵∠CAM=∠CBM=60°,∠ACM=∠ABM=60°,
∴△ACM是等边三角形,
∴AC=CM,
∴△ACB≌△MCE,
∴AB=ME,
∵ME+EB=BM,
∴AB+BC=BM.
(1)连接OA,OC,过O作OH⊥AC于点H,如图①,
∵∠ABC=120°,
∴∠AMC=180°−∠ABC=60°,
∴∠AOC=2∠AMC=120°,
∴∠AOH=1/2∠AOC=60°.
∵AH=1/2AC=√3,∠OAH=30°,
∴OH=1/2AO,
∴由勾股定理得OA=2,故⊙O的半径长为2.


(2)在BM上截取BE=BC,连接CE,如图②,
∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠CBM=60°.
∵BE=BC,
∴△EBC是等边三角形,
∴CE=CB=BE,∠BCE=60°,
∴∠BCD+∠DCE=60°.
∵∠ACM=∠ABM=60°,
∴∠ECM+∠DCE=60°,
∴∠ECM=∠BCD.
∵∠CAM=∠CBM=60°,∠ACM=∠ABM=60°,
∴△ACM是等边三角形,
∴AC=CM,
∴△ACB≌△MCE,
∴AB=ME,
∵ME+EB=BM,
∴AB+BC=BM.
3. 如图,BC为$\triangle ABC的外接圆\odot O$的直径,点M为$\triangle ABC$的内心,连接AM并延长交$\odot O$于点D,连接CD.
(1)求$\angle BCD$的大小;
(2)若$CD = 4$,求DM的长;
(3)连接OM,若$AM = 2\sqrt{2}$,$OM = \sqrt{5}$,求AC的长.
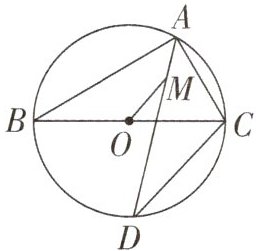
(1)求$\angle BCD$的大小;
(2)若$CD = 4$,求DM的长;
(3)连接OM,若$AM = 2\sqrt{2}$,$OM = \sqrt{5}$,求AC的长.

答案:
(1)
∵BC为△ABC的外接圆⊙O的直径,
∴∠BAC=90°.
∵M为△ABC的内心,
∴∠BAD=45°,
∴∠BCD=∠BAD=45°.
(2)如图①,连接CM,
∵M为△ABC的内心,
∴∠BAD=∠CAD,∠ACM=∠BCM.
∵⌢BD=⌢BD,
∴∠BAD=∠BCD,
∴∠DAC=∠BCD.
∵∠DMC=∠DAC+∠ACM,∠DCM=∠BCD+∠BCM,
∴∠DMC=∠DCM,
∴DM=CD=4.


(3)如图②,过M作ME⊥AB于E,MF⊥BC于F,MG⊥AC于G,则四边形AEMG是正方形,
∵点M是△ABC的内心,AM=2√2,
∴AE=AG=MF=2.在Rt△OMF中,OF=√(OM²−MF²)=√((√5)²−2²)=1.设CF=CG=x,则OC=OB=x+1,BF=BE=x+2,
∴AB=x+2+2=x+4,AC=x+2,BC=2(x+1).在Rt△ABC中,AB²+AC²=BC²,
∴(x+4)²+(x+2)²=[2(x+1)]²,解得x=4或x=−2(舍去),
∴AC=x+2=6.
(1)
∵BC为△ABC的外接圆⊙O的直径,
∴∠BAC=90°.
∵M为△ABC的内心,
∴∠BAD=45°,
∴∠BCD=∠BAD=45°.
(2)如图①,连接CM,
∵M为△ABC的内心,
∴∠BAD=∠CAD,∠ACM=∠BCM.
∵⌢BD=⌢BD,
∴∠BAD=∠BCD,
∴∠DAC=∠BCD.
∵∠DMC=∠DAC+∠ACM,∠DCM=∠BCD+∠BCM,
∴∠DMC=∠DCM,
∴DM=CD=4.


(3)如图②,过M作ME⊥AB于E,MF⊥BC于F,MG⊥AC于G,则四边形AEMG是正方形,
∵点M是△ABC的内心,AM=2√2,
∴AE=AG=MF=2.在Rt△OMF中,OF=√(OM²−MF²)=√((√5)²−2²)=1.设CF=CG=x,则OC=OB=x+1,BF=BE=x+2,
∴AB=x+2+2=x+4,AC=x+2,BC=2(x+1).在Rt△ABC中,AB²+AC²=BC²,
∴(x+4)²+(x+2)²=[2(x+1)]²,解得x=4或x=−2(舍去),
∴AC=x+2=6.
查看更多完整答案,请扫码查看


