《2025年学霸题中题九年级数学上册人教版》

10. (玉林中考)如图,正六边形ABCDEF的边长是$6+4\sqrt {3}$,点$O_{1},O_{2}分别是△ABF,△CDE$的内心,则$O_{1}O_{2}= $$12 + 4\sqrt{3}$.

答案： $12 + 4\sqrt{3}$ 解析：过点A作$AM⊥BF$于点M，连接$O_{1}F$，$O_{1}B$。
∵六边形ABCDEF是正六边形，
∴$∠BAF = 120^{\circ}$，$AF = AB$，
∴$∠AFB = ∠ABF = 30^{\circ}$，
∴$△AFB$的边BF上的高$AM = \frac{1}{2}AF = \frac{1}{2}\times(6 + 4\sqrt{3}) = 3 + 2\sqrt{3}$，$FM = BM = \frac{\sqrt{3}}{2}AF = 3\sqrt{3} + 6$，
∴$BF = 12 + 6\sqrt{3}$。设$△AFB$的内切圆的半径为r。
∵$S_{△AFB} = S_{△AO_{1}F} + S_{△AO_{1}B} + S_{△BFO_{1}}$，
∴$\frac{1}{2}\times(12 + 6\sqrt{3})\times(3 + 2\sqrt{3}) = \frac{1}{2}\times(6 + 4\sqrt{3})\times r + \frac{1}{2}\times(6 + 4\sqrt{3})\times r + \frac{1}{2}\times(12 + 6\sqrt{3})\times r$，解得$r = 3$，即$O_{1}M = r = 3$，
∴$O_{1}O_{2} = 2\times3 + 6 + 4\sqrt{3} = 12 + 4\sqrt{3}$。

11. 如图,图①、图②、图③、…、图ⓝ分别是$\odot O$的内接正三角形ABC、正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M,N分别从点B,C开始以相同的速度在$\odot O$上逆时针运动.
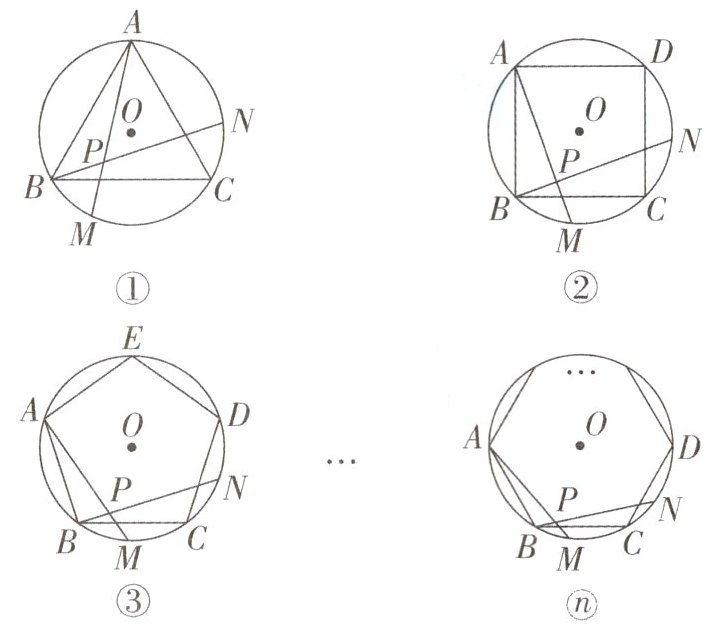
(1)图①中$∠APN$的度数是$60^{\circ}$;图②中$∠APN$的度数是$90^{\circ}$;图③中$∠APN$的度数是$108^{\circ}$.
(2)试探索$∠APN$的度数与正多边形边数n的关系(直接写出答案).

答案：
(1)$60^{\circ}$ $90^{\circ}$ $108^{\circ}$
(2)$∠APN = \frac{(n - 2)\cdot180^{\circ}}{n}$。

12. (1)如图①,已知$△ABC是\odot O$的内接正三角形,点P为$\widehat {BC}$上一动点,求证:$PA= PB+PC;$
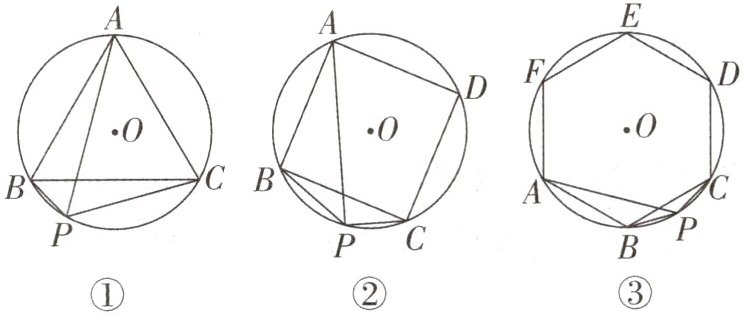
(2)如图②,四边形ABCD是$\odot O$的内接正方形,点P为$\widehat {BC}$上一动点,求证:$PA= PC+\sqrt {2}PB;$
(3)如图③,六边形ABCDEF是$\odot O$的内接正六边形,点P为$\widehat {BC}$上一动点,请探究PA,PB,PC三者之间有何数量关系,并予以证明.

答案：

(1)如图①，延长BP至E，使$PE = PC$，连接CE。由圆内接四边形的性质知$∠BAC + ∠BPC = 180^{\circ}$。
∵$∠BPC + ∠EPC = 180^{\circ}$，
∴$∠CPE = ∠BAC = 60^{\circ}$。又
∵$PE = PC$，
∴$△PCE$是正三角形，
∴$CE = PC$，$∠E = ∠PCE = 60^{\circ}$。又
∵$∠BCE = 60^{\circ} + ∠BCP$，$∠ACP = 60^{\circ} + ∠BCP$，
∴$∠BCE = ∠ACP$。
∵$△ABC$，$△ECP$都为正三角形，
∴$CE = PC$，$AC = BC$，
∴$△BEC ≌ △APC(SAS)$，
∴$PA = BE = PB + PE = PB + PC$。

(2)如图②，连接OA，OB，过点B作$BE⊥PB$交PA于点E。
∵$∠1 + ∠2 = ∠2 + ∠3 = 90^{\circ}$，
∴$∠1 = ∠3$。
∵$∠APB = \frac{1}{2}∠AOB = 45^{\circ}$，
∴$BP = BE$，
∴$PE = \sqrt{2}PB$。又
∵$AB = BC$，
∴$△ABE ≌ △CBP$，
∴$PC = AE$，
∴$PA = AE + PE = PC + \sqrt{2}PB$。
(3)$PA = \sqrt{3}PB + PC$。证明如下：如图③，过点B作$BM⊥AP$于M，在AP上截取$AQ = PC$，连接BQ。
∵$∠BAP = ∠BCP$，$AB = BC$，$AQ = CP$，
∴$△ABQ ≌ △CBP$，
∴$BQ = BP$，
∴$MP = QM$。又
∵$∠APB = 30^{\circ}$，
∴$PM = \frac{\sqrt{3}}{2}PB$，
∴$PQ = \sqrt{3}PB$，
∴$PA = PQ + AQ = \sqrt{3}PB + PC$。