第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
8. 如图,$\odot O$的半径OA,OB分别交弦CD于点E,F,且$CE= DF$.求证:$\triangle OEF$是等腰三角形.


证明:连接$OC$,$OD$,则$OC = OD$,$\therefore∠OCD = ∠ODC$。在$\triangle OCE$和$\triangle ODF$中,$\begin{cases}OC = OD,\\∠OCE = ∠ODF,\\CE = DF,\end{cases}$ $\therefore\triangle OCE\cong\triangle ODF$,$\therefore OE = OF$,$\therefore\triangle OEF$是等腰三角形。
答案:
连接$OC$,$OD$,则$OC = OD$,$\therefore∠OCD = ∠ODC$。在$\triangle OCE$和$\triangle ODF$中,$\begin{cases}OC = OD,\\∠OCE = ∠ODF,\\CE = DF,\end{cases}$ $\therefore\triangle OCE\cong\triangle ODF$,$\therefore OE = OF$,$\therefore\triangle OEF$是等腰三角形。
9. (随州中考改编)如图,点A,B,C在$\odot O$上,$∠A= 40^{\circ },∠C= 20^{\circ }$,则$∠B$的度数为 (
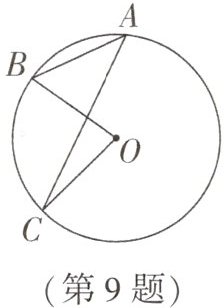
A. $30^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $80^{\circ }$
C
)
A. $30^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $80^{\circ }$
答案:
C
归纳总结
连半径构等腰或全等:同圆或等圆中半径相等,因此我们常常连接半径,构造等腰三角形或全等三角形解题。
归纳总结
连半径构等腰或全等:同圆或等圆中半径相等,因此我们常常连接半径,构造等腰三角形或全等三角形解题。
10. (2024·宁波月考)如图,在$\odot O$中,直径$MN= 20$,正方形ABCD的四个顶点分别在半径OP,OM及$\odot O$上,且$∠POM= 45^{\circ }$,则$AB= $ ( )

A. 4
B. $2\sqrt {5}$
C. $2\sqrt {6}$
D. 6

A. 4
B. $2\sqrt {5}$
C. $2\sqrt {6}$
D. 6
答案:
B 解析:连接$OA$,如图,$\because$四边形$ABCD$是正方形,$\therefore AB = BC = CD$,$∠ABC = ∠BCD = 90^{\circ}$,$\therefore∠DCO = 180^{\circ} - ∠BCD = 90^{\circ}$。$\because∠POM = 45^{\circ}$,$\therefore∠CDO = 90^{\circ} - ∠POM = 45^{\circ}$,$\therefore∠CDO = ∠POM$,$\therefore CO = CD$。$\because$直径$MN = 20$,$\therefore OA = \frac{1}{2}MN = 10$,设$AB = BC = CD = CO = x$,则$BO = BC + CO = 2x$。在$Rt\triangle ABO$中,由勾股定理得$AB^{2} + BO^{2} = OA^{2}$,即$x^{2} + (2x)^{2} = 10^{2}$,解得$x = 2\sqrt{5}$或$x = -2\sqrt{5}$(舍去),$\therefore AB = 2\sqrt{5}$。

B 解析:连接$OA$,如图,$\because$四边形$ABCD$是正方形,$\therefore AB = BC = CD$,$∠ABC = ∠BCD = 90^{\circ}$,$\therefore∠DCO = 180^{\circ} - ∠BCD = 90^{\circ}$。$\because∠POM = 45^{\circ}$,$\therefore∠CDO = 90^{\circ} - ∠POM = 45^{\circ}$,$\therefore∠CDO = ∠POM$,$\therefore CO = CD$。$\because$直径$MN = 20$,$\therefore OA = \frac{1}{2}MN = 10$,设$AB = BC = CD = CO = x$,则$BO = BC + CO = 2x$。在$Rt\triangle ABO$中,由勾股定理得$AB^{2} + BO^{2} = OA^{2}$,即$x^{2} + (2x)^{2} = 10^{2}$,解得$x = 2\sqrt{5}$或$x = -2\sqrt{5}$(舍去),$\therefore AB = 2\sqrt{5}$。

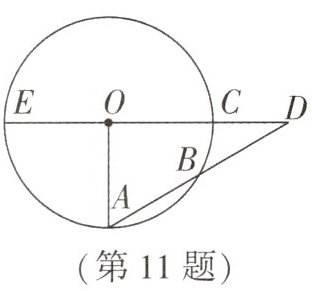
11. 原创题 如图,点A为$\odot O$上一动点,点D为圆外一点,AD交$\odot O$于点B,OD交$\odot O$于点C,延长DO交$\odot O$于点E.
(1)若$∠AOD= 90^{\circ },AD= 8$,点B恰为AD的中点,则OD的长为____
(2)若$∠AOE= 99^{\circ },BD= OA$,则$∠ODA= $____
(1)若$∠AOD= 90^{\circ },AD= 8$,点B恰为AD的中点,则OD的长为____
$4\sqrt{3}$
.(2)若$∠AOE= 99^{\circ },BD= OA$,则$∠ODA= $____
$33^{\circ}$
.
答案:
(1) $4\sqrt{3}$
(2) $33^{\circ}$
(1) $4\sqrt{3}$
(2) $33^{\circ}$
12. (2024·西安期末)如图,AB为$\odot O$的直径,点C,D在$\odot O$上,若$∠AOD= 28^{\circ }$,则$∠BCD= $____.
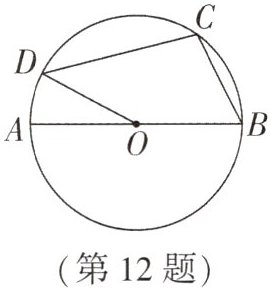

答案:
$104^{\circ}$ 解析:如图,连接$OC$,$\because OD = OC$,$OC = OB$,$\therefore∠D = ∠OCD$,$∠B = ∠OCB$,$\therefore∠OCD = \frac{180^{\circ} - ∠DOC}{2}$,$∠OCB = \frac{180^{\circ} - ∠BOC}{2}$,$\therefore∠BCD = \frac{180^{\circ} - ∠DOC}{2} + \frac{180^{\circ} - ∠BOC}{2} = 180^{\circ} - \frac{1}{2}(∠DOC + ∠BOC) = 180^{\circ} - \frac{1}{2}∠BOD$。$\because∠AOD = 28^{\circ}$,$AB$为$\odot O$的直径,$\therefore∠BOD = 152^{\circ}$,$\therefore∠BCD = 180^{\circ} - \frac{1}{2}∠BOD = 104^{\circ}$。

$104^{\circ}$ 解析:如图,连接$OC$,$\because OD = OC$,$OC = OB$,$\therefore∠D = ∠OCD$,$∠B = ∠OCB$,$\therefore∠OCD = \frac{180^{\circ} - ∠DOC}{2}$,$∠OCB = \frac{180^{\circ} - ∠BOC}{2}$,$\therefore∠BCD = \frac{180^{\circ} - ∠DOC}{2} + \frac{180^{\circ} - ∠BOC}{2} = 180^{\circ} - \frac{1}{2}(∠DOC + ∠BOC) = 180^{\circ} - \frac{1}{2}∠BOD$。$\because∠AOD = 28^{\circ}$,$AB$为$\odot O$的直径,$\therefore∠BOD = 152^{\circ}$,$\therefore∠BCD = 180^{\circ} - \frac{1}{2}∠BOD = 104^{\circ}$。

13. 如图,四边形ADFE和四边形BCDG都为正方形,且点F,D,C在半圆O的直径上,点E,A,B在半圆O的圆弧上,若小正方形的面积为$16cm^{2}$,求该半圆的半径.
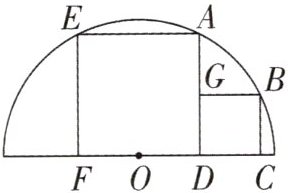

答案:
如图,连接$OA$,$OB$,$OE$。$\because$四边形$ADFE$为正方形,$\therefore EF = AD$,$∠EFO = ∠ADO = 90^{\circ}$。又$\because OE = OA$,$\therefore\triangle OEF\cong\triangle OAD$,$\therefore OF = OD$。$\because$小正方形的面积为$16cm^{2}$,$\therefore DC = CB = BG = GD = 4cm$,设$OD = xcm$,则$OC = (x + 4)cm$,$AD = DF = 2xcm$。在$Rt\triangle AOD$中,$OA^{2} = OD^{2} + AD^{2} = x^{2} + (2x)^{2} = 5x^{2}$,在$Rt\triangle OBC$中,$OB^{2} = OC^{2} + BC^{2} = (x + 4)^{2} + 4^{2}$。$\because OA = OB$,$\therefore(x + 4)^{2} + 4^{2} = 5x^{2}$,整理得$x^{2} - 2x - 8 = 0$,解得$x_{1} = 4$,$x_{2} = -2$(舍去),$\therefore OA = \sqrt{5}x = 4\sqrt{5}cm$,即该半圆的半径为$4\sqrt{5}cm$。

如图,连接$OA$,$OB$,$OE$。$\because$四边形$ADFE$为正方形,$\therefore EF = AD$,$∠EFO = ∠ADO = 90^{\circ}$。又$\because OE = OA$,$\therefore\triangle OEF\cong\triangle OAD$,$\therefore OF = OD$。$\because$小正方形的面积为$16cm^{2}$,$\therefore DC = CB = BG = GD = 4cm$,设$OD = xcm$,则$OC = (x + 4)cm$,$AD = DF = 2xcm$。在$Rt\triangle AOD$中,$OA^{2} = OD^{2} + AD^{2} = x^{2} + (2x)^{2} = 5x^{2}$,在$Rt\triangle OBC$中,$OB^{2} = OC^{2} + BC^{2} = (x + 4)^{2} + 4^{2}$。$\because OA = OB$,$\therefore(x + 4)^{2} + 4^{2} = 5x^{2}$,整理得$x^{2} - 2x - 8 = 0$,解得$x_{1} = 4$,$x_{2} = -2$(舍去),$\therefore OA = \sqrt{5}x = 4\sqrt{5}cm$,即该半圆的半径为$4\sqrt{5}cm$。

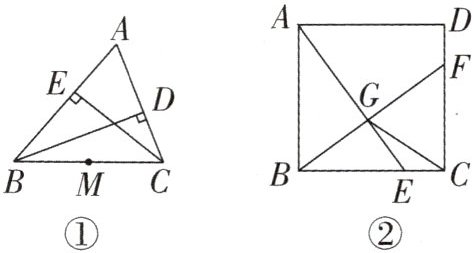
14. 教材P81练习T3拓展 改编题 人教数学课本上有这样一道练习题:“$\triangle ABC$中,$∠C= 90^{\circ }$.求证:A,B,C三点在同一个圆上”.下面我们进一步探究.
(1)如图①,BD,CE是$\triangle ABC$的高,M是BC的中点,求证:点B,C,D,E在同一个圆上;
(2)如图②,已知正方形ABCD的边长为2,E是BC边上的动点,$BF⊥AE$交CD于点F,垂足为G,连接CG.求CG的最小值.
(1)如图①,BD,CE是$\triangle ABC$的高,M是BC的中点,求证:点B,C,D,E在同一个圆上;
(2)如图②,已知正方形ABCD的边长为2,E是BC边上的动点,$BF⊥AE$交CD于点F,垂足为G,连接CG.求CG的最小值.

答案:
(1)如图①,连接$ME$,$MD$,$\because BD$,$CE$分别是$\triangle ABC$的高,$M$为$BC$的中点,$\therefore ME = MD = MC = MB = \frac{1}{2}BC$,$\therefore$点$B$,$C$,$D$,$E$在以点$M$为圆心的同一个圆上。

(2)如图②,取$AB$的中点$O$,连接$OC$,$OG$,则$OG = \frac{1}{2}AB = OA = OB$,$\therefore$根据题意,$G$点的轨迹是以点$O$为圆心,$AO$为半径的圆弧,$\therefore OC$和$OG$的长度是一定的,因此当$O$,$G$,$C$三点在同一条直线上时,$CG$取最小值。$\because$正方形$ABCD$的边长为$2$,$∠ABC = 90^{\circ}$,$\therefore OB = 1$,$BC = 2$,$\therefore OC = \sqrt{5}$,$\therefore CG$的最小值为$OC - OG = \sqrt{5} - 1$。

归纳总结
隐圆问题:有时候,题目条件中没有直接给出圆的信息,而是将其隐藏在题目中,要通过分析和转化,发现或构造圆,我们把这类问题称为隐圆问题。根据圆的定义,到定点的距离等于定长的点都在同一个圆上,利用“直角三角形斜边上的中线等于斜边的一半”,我们可以得知直角三角形的三个顶点在同一个圆上,进而得到共斜边的两个直角三角形四个顶点共圆。
(1)如图①,连接$ME$,$MD$,$\because BD$,$CE$分别是$\triangle ABC$的高,$M$为$BC$的中点,$\therefore ME = MD = MC = MB = \frac{1}{2}BC$,$\therefore$点$B$,$C$,$D$,$E$在以点$M$为圆心的同一个圆上。

(2)如图②,取$AB$的中点$O$,连接$OC$,$OG$,则$OG = \frac{1}{2}AB = OA = OB$,$\therefore$根据题意,$G$点的轨迹是以点$O$为圆心,$AO$为半径的圆弧,$\therefore OC$和$OG$的长度是一定的,因此当$O$,$G$,$C$三点在同一条直线上时,$CG$取最小值。$\because$正方形$ABCD$的边长为$2$,$∠ABC = 90^{\circ}$,$\therefore OB = 1$,$BC = 2$,$\therefore OC = \sqrt{5}$,$\therefore CG$的最小值为$OC - OG = \sqrt{5} - 1$。

归纳总结
隐圆问题:有时候,题目条件中没有直接给出圆的信息,而是将其隐藏在题目中,要通过分析和转化,发现或构造圆,我们把这类问题称为隐圆问题。根据圆的定义,到定点的距离等于定长的点都在同一个圆上,利用“直角三角形斜边上的中线等于斜边的一半”,我们可以得知直角三角形的三个顶点在同一个圆上,进而得到共斜边的两个直角三角形四个顶点共圆。
查看更多完整答案,请扫码查看


