第134页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
1. 如图,半径为 5 的半圆的初始状态是直径平行于桌面上的直线 b,然后把半圆沿直线 b 进行无滑动滚动,使半圆的直径与直线 b 重合为止,则圆心 O 运动路径的长度等于(
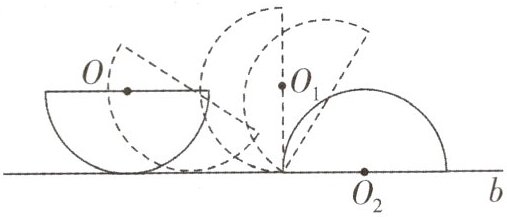
A. $5\pi$
B. $2.5\pi$
C. $5 + 2.5\pi$
D. 10
A
)
A. $5\pi$
B. $2.5\pi$
C. $5 + 2.5\pi$
D. 10
答案:
A
2. (2025·西安期末)如图,用一个半径为 3 cm 的定滑轮带动重物上升,滑轮上一点 P 旋转了 $90^{\circ}$,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了
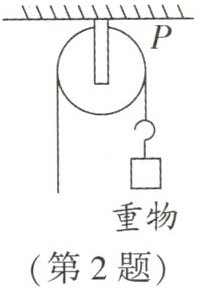
$\frac{3\pi}{2}$
cm.(结果保留 $\pi$)
答案:
$\frac{3\pi}{2}$
3. (2024·南京模拟)在活动课上,“雄鹰组”用含 $30^{\circ}$角的直角三角尺设计风车,如图,$\angle C = 90^{\circ}$,$\angle ABC = 30^{\circ}$,$AC = 2$,将直角三角尺绕点 A 逆时针旋转得到 $\triangle AB'C'$,使点 $C'$落在 AB 边上,以此方法做下去……则点 B 通过一次旋转至点 $B'$所经过的路径长为
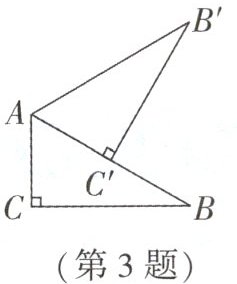
$\frac{4\pi}{3}$
.(结果保留 $\pi$)
答案:
$\frac{4\pi}{3}$
4. (2025·南昌期末)如图,直角三角板放置在平面直角坐标系上,$\angle BAO = 30^{\circ}$,将三角板绕点 $A(\sqrt{3},0)$顺时针旋转到如图位置,则点 B 旋转过程弧长为______

$\frac{5\pi}{3}$
.(结果保留 $\pi$)
答案:
$\frac{5\pi}{3}$
5. 如图,在扇形 OAB 中,$\angle AOB = 60^{\circ}$,扇形半径为 r,点 C 在 $\overset{\frown}{AB}$上,$CD \perp OA$,垂足为点 D,当 $\triangle OCD$的面积最大时,$\overset{\frown}{AC}$的长为
$\frac{1}{4}\pi r$
.
答案:
$\frac{1}{4}\pi r$
6. 一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为 10 cm 的圆盘,如图所示,AB 与 CD 是平行的,且水平,BC 与水平面的夹角为 $60^{\circ}$,其中 $AB = 60$ cm,$BC = 40$ cm,$CD = 40$ cm,请你作出该小朋友将圆盘从点 A 滚动到点 D 其圆心所经过的路线的示意图,并求出此路线的长度.
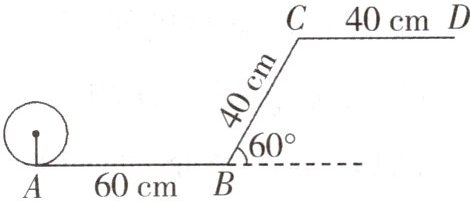

答案:
如图所示是圆盘滚动过程中,其圆心所经过的路线的示意图。

由图知圆盘滚动过程中,其圆心经过的路线由线段 $OO_1$,线段 $O_1O_2$,$\overset{\frown}{O_2O_3}$,线段 $O_3O_4$ 四部分构成。其中 $O_1E\perp AB$,$O_1F\perp BC$,$O_2C\perp BC$,$O_3C\perp CD$,$O_4D\perp CD$。$\because BC$ 与 $AB$ 延长线的夹角为 $60^{\circ}$,$O_1$ 是圆盘在 $AB$ 上滚动到与 $BC$ 相切时的圆心位置,$\therefore$ 此时 $\odot O_1$ 与 $AB$ 和 $BC$ 都相切,则 $\angle O_1BE = \angle O_1BF = 60^{\circ}$。此时 $Rt\triangle O_1BE\cong Rt\triangle O_1BF$,在 $Rt\triangle O_1BE$ 中,$BE = \frac{10\sqrt{3}}{3}cm$,$\therefore OO_1 = AE = AB - BE = (60 - \frac{10\sqrt{3}}{3})cm$。$\because BF = BE = \frac{10\sqrt{3}}{3}cm$,$\therefore O_1O_2 = CF = BC - BF = (40 - \frac{10\sqrt{3}}{3})cm$。$\because AB// CD$,$BC$ 与水平面的夹角为 $60^{\circ}$,$\therefore \angle BCD = 120^{\circ}$。又 $\angle O_2CB = \angle O_3CD = 90^{\circ}$,$\therefore \angle O_2CO_3 = 60^{\circ}$。则圆盘在点 $C$ 处滚动,其圆心所经过的路线为圆心角为 $60^{\circ}$ 且半径为 $10cm$ 的圆弧 $\overset{\frown}{O_2O_3}$,$\therefore \overset{\frown}{O_2O_3}$ 的长为 $\frac{60\times \pi\times 10}{180} = \frac{10}{3}\pi(cm)$。$\because$ 四边形 $O_3O_4DC$ 是矩形,$\therefore O_3O_4 = CD = 40cm$。综上所述,圆盘从点 $A$ 滚动到点 $D$ 其圆心所经过的路线的长度是 $(60 - \frac{10\sqrt{3}}{3}) + (40 - \frac{10\sqrt{3}}{3}) + \frac{10}{3}\pi + 40 = (140 - \frac{20\sqrt{3}}{3} + \frac{10}{3}\pi)cm$。
如图所示是圆盘滚动过程中,其圆心所经过的路线的示意图。

由图知圆盘滚动过程中,其圆心经过的路线由线段 $OO_1$,线段 $O_1O_2$,$\overset{\frown}{O_2O_3}$,线段 $O_3O_4$ 四部分构成。其中 $O_1E\perp AB$,$O_1F\perp BC$,$O_2C\perp BC$,$O_3C\perp CD$,$O_4D\perp CD$。$\because BC$ 与 $AB$ 延长线的夹角为 $60^{\circ}$,$O_1$ 是圆盘在 $AB$ 上滚动到与 $BC$ 相切时的圆心位置,$\therefore$ 此时 $\odot O_1$ 与 $AB$ 和 $BC$ 都相切,则 $\angle O_1BE = \angle O_1BF = 60^{\circ}$。此时 $Rt\triangle O_1BE\cong Rt\triangle O_1BF$,在 $Rt\triangle O_1BE$ 中,$BE = \frac{10\sqrt{3}}{3}cm$,$\therefore OO_1 = AE = AB - BE = (60 - \frac{10\sqrt{3}}{3})cm$。$\because BF = BE = \frac{10\sqrt{3}}{3}cm$,$\therefore O_1O_2 = CF = BC - BF = (40 - \frac{10\sqrt{3}}{3})cm$。$\because AB// CD$,$BC$ 与水平面的夹角为 $60^{\circ}$,$\therefore \angle BCD = 120^{\circ}$。又 $\angle O_2CB = \angle O_3CD = 90^{\circ}$,$\therefore \angle O_2CO_3 = 60^{\circ}$。则圆盘在点 $C$ 处滚动,其圆心所经过的路线为圆心角为 $60^{\circ}$ 且半径为 $10cm$ 的圆弧 $\overset{\frown}{O_2O_3}$,$\therefore \overset{\frown}{O_2O_3}$ 的长为 $\frac{60\times \pi\times 10}{180} = \frac{10}{3}\pi(cm)$。$\because$ 四边形 $O_3O_4DC$ 是矩形,$\therefore O_3O_4 = CD = 40cm$。综上所述,圆盘从点 $A$ 滚动到点 $D$ 其圆心所经过的路线的长度是 $(60 - \frac{10\sqrt{3}}{3}) + (40 - \frac{10\sqrt{3}}{3}) + \frac{10}{3}\pi + 40 = (140 - \frac{20\sqrt{3}}{3} + \frac{10}{3}\pi)cm$。
查看更多完整答案,请扫码查看


