第99页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
1. 如图,$l_{1}$反映了某种产品的销售收入与销售量的关系,$l_{2}$反映了该种产品的销售成本与销售量的关系. 根据图象提供的信息,下列说法正确的是(
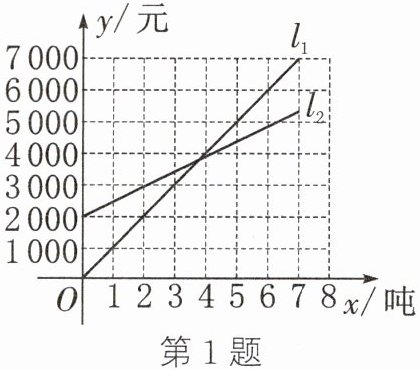
A. 当销售量为2吨时,销售成本是2000元
B. 销售成本是3000元时,该产品盈利
C. 当销售量为5吨时,该产品盈利1000元
D. $l_{1}的函数表达式为y = 1000x$
D
)
A. 当销售量为2吨时,销售成本是2000元
B. 销售成本是3000元时,该产品盈利
C. 当销售量为5吨时,该产品盈利1000元
D. $l_{1}的函数表达式为y = 1000x$
答案:
D
2. 甲车从A城出发匀速行驶至B城,乙车从B城出发匀速行驶至A城,在整个行驶过程中,甲、乙两车距离A城的距离$y(km)与甲车行驶的时间t(h)$之间的函数关系如图所示,下列结论错误的是(

A. A、B两城相距360km
B. 乙车比甲车晚出发1h
C. 甲、乙两车相遇时甲车行驶了2.5h
D. 当甲、乙两车相距96km时,$t = 2$
D
)
A. A、B两城相距360km
B. 乙车比甲车晚出发1h
C. 甲、乙两车相遇时甲车行驶了2.5h
D. 当甲、乙两车相距96km时,$t = 2$
答案:
D
3. 已知A、B两地相距10km,上午9:00甲骑电动车从A地出发到B地,9:10乙开车从B地出发到A地,甲、乙两人距A地的距离$y(km)与甲所用的时间x(min)$之间的关系如图所示,则乙到达A地的时间为______

9:20
.
答案:
9:20
4. 某塑料生产公司为做好转型升级,经过市场研究购进一批可降解吸管生产设备,并分别绘制出了吸管的销售收入$y_{1}$(万元)和吸管的销售成本$y_{2}$(万元)与销售量$x(t)$的关系,如图所示.
(1)求函数$y_{1}$和$y_{2}$的表达式;
(2)当销售量$x$满足条件
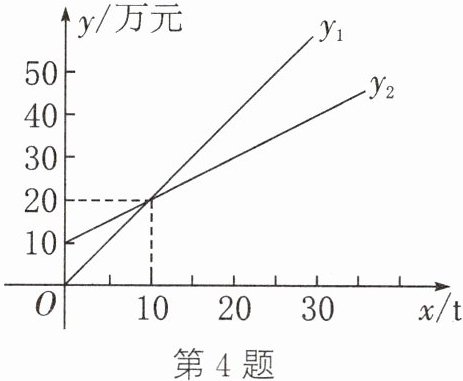
(1)求函数$y_{1}$和$y_{2}$的表达式;
(2)当销售量$x$满足条件
$x > 10$
时,该公司盈利(即销售收入大于销售成本).
答案:
解:
(1) 设 $ y_1 $ 与 $ x $ 的函数关系式为 $ y_1 = kx $,
∵ 点 $ (10, 20) $ 在该函数图象上,
∴ $ 10k = 20 $,得 $ k = 2 $,即 $ y_1 $ 与 $ x $ 的函数关系式为 $ y_1 = 2x $;设 $ y_2 $ 与 $ x $ 的函数关系式为 $ y_2 = cx + d $,$ \begin{cases} d = 10, \\ 10c + d = 20, \end{cases} $ 解得 $ \begin{cases} c = 1, \\ d = 10, \end{cases} $ 即 $ y_2 $ 与 $ x $ 的函数关系式为 $ y_2 = x + 10 $;
(2) $ x > 10 $
(1) 设 $ y_1 $ 与 $ x $ 的函数关系式为 $ y_1 = kx $,
∵ 点 $ (10, 20) $ 在该函数图象上,
∴ $ 10k = 20 $,得 $ k = 2 $,即 $ y_1 $ 与 $ x $ 的函数关系式为 $ y_1 = 2x $;设 $ y_2 $ 与 $ x $ 的函数关系式为 $ y_2 = cx + d $,$ \begin{cases} d = 10, \\ 10c + d = 20, \end{cases} $ 解得 $ \begin{cases} c = 1, \\ d = 10, \end{cases} $ 即 $ y_2 $ 与 $ x $ 的函数关系式为 $ y_2 = x + 10 $;
(2) $ x > 10 $
查看更多完整答案,请扫码查看


