第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
12. 如图①,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,人只要移至该门口4m及4m以内时,门铃就会自动发出语音“欢迎光临”.如图②,一个身高1.5m的学生刚走到D处,门铃恰好自动响起,则该生头顶C到门铃A的距离为____

5m
.
答案:
5m
13. 如图,在$△ABC$中,$∠A= 90^{\circ },BC= 5,AB= 3$,线段BC的垂直平分线分别交AC、BC于点P和Q,则PA的长度为

$\frac{7}{8}$
.
答案:
$\frac{7}{8}$
14. 如图是$2×4$正方形网格图,点A、B、C、D、E都是格点,则$∠BAC-∠BDE= $
45
°.
答案:
45
15. 如图,已知$AB= 12,AB⊥BC$于点B,$AB⊥AD$于点A,$AD= 5,BC= 10$,E是CD的中点.求AE的长.

解:延长 AE 交 BC 于 F. ∵ $AB⊥BC$,$AB⊥AD$,∴ $AD// BC$. ∴ $∠D = ∠C$,$∠DAE = ∠CFE$. 又 ∵ 点 E 是 CD 的中点,∴ $DE = CE$. ∵ 在 $△AED$ 与 $△FEC$ 中,$\left\{\begin{array}{l} ∠D = ∠C,\\ ∠DAE = ∠CFE,\\ DE = CE,\end{array}\right.$ ∴ $△AED≌△FEC$. ∴ $AE = FE$,$AD = FC$. ∵ $AD = 5$,$BC = 10$. ∴ $BF = 5$. 在 $Rt△ABF$ 中,$AF^{2} = AB^{2} + BF^{2}$. ∴ $AF = 13$. ∴ $AE =$

解:延长 AE 交 BC 于 F. ∵ $AB⊥BC$,$AB⊥AD$,∴ $AD// BC$. ∴ $∠D = ∠C$,$∠DAE = ∠CFE$. 又 ∵ 点 E 是 CD 的中点,∴ $DE = CE$. ∵ 在 $△AED$ 与 $△FEC$ 中,$\left\{\begin{array}{l} ∠D = ∠C,\\ ∠DAE = ∠CFE,\\ DE = CE,\end{array}\right.$ ∴ $△AED≌△FEC$. ∴ $AE = FE$,$AD = FC$. ∵ $AD = 5$,$BC = 10$. ∴ $BF = 5$. 在 $Rt△ABF$ 中,$AF^{2} = AB^{2} + BF^{2}$. ∴ $AF = 13$. ∴ $AE =$
6.5
.
答案:
解:延长 AE 交 BC 于 F.
∵ $AB⊥BC$,$AB⊥AD$,
∴ $AD// BC$.
∴ $∠D = ∠C$,$∠DAE = ∠CFE$. 又
∵ 点 E 是 CD 的中点,
∴ $DE = CE$.
∵ 在 $△AED$ 与 $△FEC$ 中,$\left\{\begin{array}{l} ∠D = ∠C,\\ ∠DAE = ∠CFE,\\ DE = CE,\end{array}\right.$
∴ $△AED≌△FEC$.
∴ $AE = FE$,$AD = FC$.
∵ $AD = 5$,$BC = 10$.
∴ $BF = 5$. 在 $Rt△ABF$ 中,$AF^{2} = AB^{2} + BF^{2}$.
∴ $AF = 13$.
∴ $AE = 6.5$.
∵ $AB⊥BC$,$AB⊥AD$,
∴ $AD// BC$.
∴ $∠D = ∠C$,$∠DAE = ∠CFE$. 又
∵ 点 E 是 CD 的中点,
∴ $DE = CE$.
∵ 在 $△AED$ 与 $△FEC$ 中,$\left\{\begin{array}{l} ∠D = ∠C,\\ ∠DAE = ∠CFE,\\ DE = CE,\end{array}\right.$
∴ $△AED≌△FEC$.
∴ $AE = FE$,$AD = FC$.
∵ $AD = 5$,$BC = 10$.
∴ $BF = 5$. 在 $Rt△ABF$ 中,$AF^{2} = AB^{2} + BF^{2}$.
∴ $AF = 13$.
∴ $AE = 6.5$.
16. 拖拉机行驶过程中会对周围产生较大的噪声影响.如图,有一台拖拉机沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A、B的距离分别为150m和200m,又$AB= 250m$,拖拉机周围130m以内为受噪声影响区域.
(1)学校C会受噪声影响吗?为什么?
(2)若拖拉机的行驶速度为每分钟50m,拖拉机噪声影响该学校持续的时间有多少分钟?
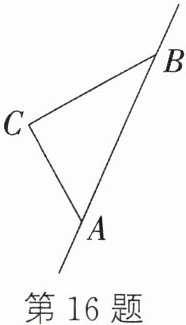
(1)学校C会受噪声影响吗?为什么?
(2)若拖拉机的行驶速度为每分钟50m,拖拉机噪声影响该学校持续的时间有多少分钟?

答案:
解:
(1) 学校 C 会受噪声影响. 理由:如图,过点 C 作 $CD⊥AB$ 于点 D,
∵ $AC = 150m$,$BC = 200m$,$AB = 250m$,
∴ $AC^{2} + BC^{2} = AB^{2}$.
∴ $△ABC$ 是直角三角形.
∴ $AC×BC = CD×AB$.
∴ $150×200 = 250×CD$.
∴ $CD = \frac{150×200}{250} = 120(m)$.
∵ 拖拉机周围 130m 以内为受噪声影响区域,
∴ 学校 C 会受噪声影响;
(2) 当 $EC = 130m$,$FC = 130m$ 时,正好影响 C 学校,
∵ $ED^{2} = EC^{2} - CD^{2} = 130^{2} - 120^{2}$,
∴ $ED = 50m$.
∴ $EF = 100m$.
∵ 拖拉机的行驶速度为每分钟 50m,
∴ $100÷50 = 2$(分钟),即拖拉机噪声影响该学校持续的时间有 2 分钟.

解:
(1) 学校 C 会受噪声影响. 理由:如图,过点 C 作 $CD⊥AB$ 于点 D,
∵ $AC = 150m$,$BC = 200m$,$AB = 250m$,
∴ $AC^{2} + BC^{2} = AB^{2}$.
∴ $△ABC$ 是直角三角形.
∴ $AC×BC = CD×AB$.
∴ $150×200 = 250×CD$.
∴ $CD = \frac{150×200}{250} = 120(m)$.
∵ 拖拉机周围 130m 以内为受噪声影响区域,
∴ 学校 C 会受噪声影响;
(2) 当 $EC = 130m$,$FC = 130m$ 时,正好影响 C 学校,
∵ $ED^{2} = EC^{2} - CD^{2} = 130^{2} - 120^{2}$,
∴ $ED = 50m$.
∴ $EF = 100m$.
∵ 拖拉机的行驶速度为每分钟 50m,
∴ $100÷50 = 2$(分钟),即拖拉机噪声影响该学校持续的时间有 2 分钟.

查看更多完整答案,请扫码查看


