《2025年轻松作业本八年级数学上册苏科版》

8. 在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点$A_{1}$,第二次移动到点$A_{2}$……第n次移动到点$A_{n}$,则点$A_{2025}$的坐标是 (C)

A. $(1011,0)$
B. $(1011,1)$
C. $(1012,1)$
D. $(1012,0)$

答案： C

9. 如图,已知点A、B的坐标分别为$(1,2)$、$(3,0)$,将$△OAB$沿x轴向右平移,使点B平移到点E,得到$△DCE$,若$OE= 5$,则点C的坐标为____(3,2).

答案： $(3,2)$

10. 已知点M坐标为$(3a-9,-3)$,将点M向左平移3个单位长度后落在y轴上,则a的值为____4.

答案： 4

11. 已知点$P(0,-4),Q(6,1)$,将线段PQ平移至$P_{1}Q_{1}$,点P、Q的对应点分别为点$P_{1}$、$Q_{1}$,若$P_{1}(m,-3),Q_{1}(3,n)$,则$m-n$的值是-5.

答案： $-5$

12. 对于平面直角坐标系中的任意一点$P(x,y)$,给出如下定义:点$P_{1}(x+1,2y-1)$为P的1号派生点,点$P_{2}(-y,-x)$为P的2号派生点,例如$P(2,3)$的1号派生点为$P_{1}(3,5)$,它的2号派生点为$P_{2}(-3,-2)$.
(1) 已知点$P(2,4)$,那么它的1号派生点为$(3,7)$,2号派生点为$(-4,-2)$;
(2) 若将点P向上平移1个单位长度,分别直接写出$P_{1}和P_{2}$的平移方向和距离;$P_{1}$的平移方向为向上，平移距离为2个单位，$P_{2}$的平移方向为向左，平移距离为1个单位
(3) 已知点$P(-m,2m)$,连接它的1号派生点$P_{1}$和2号派生点$P_{2}$,若线段$P_{1}P_{2}$平行于坐标轴,求m的值.$\frac{1}{3}$或$-1$

答案： 解：
(1)
∵点$P(2,4)$，
∴它的1号派生点为$(3,7)$，2号派生点为$(-4,-2)$；
(2)将点P向上平移1个单位长度，所得点的坐标为$(x,y+1)$，
∴1号派生点$P_{1}(x+1,2y-1)$平移后的坐标为$(x+1,2(y+1)-1)$，即$(x+1,2y+1)$，2号派生点$P_{2}(-y,-x)$平移后的坐标为$(-y-1,-x)$，
∴$P_{1}$的平移方向为向上，平移距离为2个单位，$P_{2}$的平移方向为向左，平移距离为1个单位；
(3)
∵$P(-m,2m)$，
∴$P_{1}(-m+1,4m-1)$，$P_{2}(-2m,m)$，当线段$P_{1}P_{2}$平行于x轴时，$4m-1=m$，解得$m=\frac{1}{3}$；当线段$P_{1}P_{2}$平行于y轴时，$-m+1=-2m$，解得$m=-1$，综上所述，m的值为$\frac{1}{3}$或$-1$。

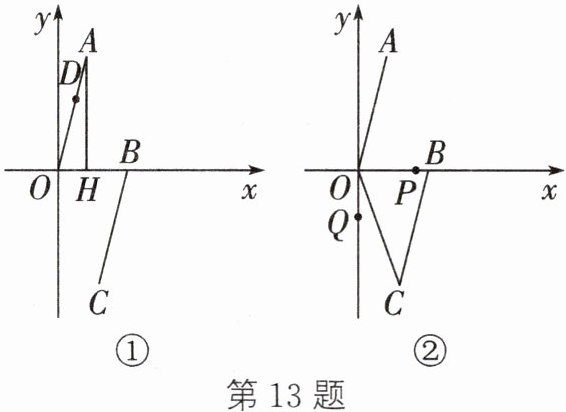
13. 如图①,点$A(1,4),AH⊥x$轴,垂足为H,将线段AO平移至线段BC,点$B(3,0)$,其中点A与点B对应,点O与点C对应.
(1)$△AOH$的面积为____2;
(2) 如图①,若点$D(m,n)$在线段OA上,连接DH,利用图形面积关系证明$n= 4m$;
(3) 如图②,连接OC,动点P从点B开始在x轴上以每秒2个单位长度的速度向左运动,同时点Q从点O开始在y轴上以每秒1个单位长度的速度向下运动.若经过t秒,$△AOP与△COQ$的面积相等,试求t的值及点P的坐标.当点P在y轴的右侧时，$t=\frac{6}{5}$，此时$P(\frac{3}{5},0)$；当点P在y轴的左侧时，$t=2$，此时$P(-1,0)$

答案： 解：
(1)2
(2)解：连接DH，$S_{\triangle AOH}=S_{\triangle ADH}+S_{\triangle ODH}=\frac{1}{2}×1×n+\frac{1}{2}×4×(1-m)=\frac{1}{2}n+2-2m$；由
(1)知$S_{\triangle AOH}=2$，
∴$2=\frac{1}{2}n+2-2m$，
∴$n=4m$；
(3)当点P在y轴的右侧时，$\frac{1}{2}×(3-2t)×4=\frac{1}{2}×t×2$，解得，$t=\frac{6}{5}$，此时$P(\frac{3}{5},0)$，当点P在y轴的左侧时，$\frac{1}{2}×(2t-3)×4=\frac{1}{2}×t×2$，解得，$t=2$，此时$P(-1,0)$。