《2025年轻松作业本八年级数学上册苏科版》

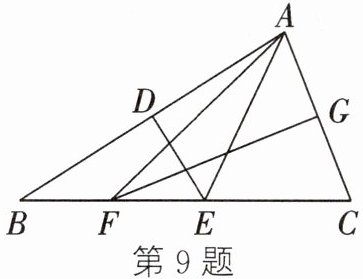
9. 如图,在$ △ABC $中,AB的垂直平分线DE分别与AB、BC交于点D、E,AC的垂直平分线FG分别与BC、AC交于点F、G,$ BC = 10 $,$ EF = 3 $,则$ △AEF $的周长是(D)

A. 7
B. 10
C. 13
D. 16

答案： D

10. 如图,在$ △ABC $中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若$ AD = 3 $,$ △ABC $的周长为15,则$ △ACE $的周长是______9.

答案： 9

11. 如图,已知AB比AC长3cm,BC的垂直平分线交AB于点D,交BC于点E,$ △ACD $的周长是14cm,求AB和AC的长.

解：∵ DE是BC的垂直平分线，∴ $ CD = $BD. ∴ $ \triangle ACD $ 的周长 $ = AC + AD + CD = AC + $BD$ + AD = AC + $AB. 由题意得，$ AB - AC = $3，$ AB + AC = $14，解得：$ AC = $5.5，$ AB = $8.5.

答案： 解：
∵ DE是BC的垂直平分线，
∴ $ CD = BD $.
∴ $ \triangle ACD $ 的周长 $ = AC + AD + CD = AC + BD + AD = AC + AB $. 由题意得，$ AB - AC = 3 $，$ AB + AC = 14 $，解得：$ AC = 5.5 $，$ AB = 8.5 $.

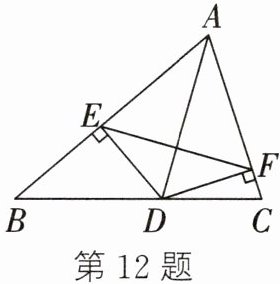
12. 如图,AD是$ △ABC $的角平分线,DE、DF分别是$ △ABD $和$ △ACD $的高.
求证：AD垂直平分EF.

证明：设AD、EF的交点为K，∵ AD平分$ \angle BAC $，$ DE \perp AB $，$ DF \perp AC $，∴ $ DE = DF $. ∵ $ DE \perp AB $，$ DF \perp AC $，∴ $ \angle AED = \angle AFD = 90^\circ $. 在 $ Rt\triangle ADE $ 和 $ Rt\triangle ADF $ 中，$ AD = AD $，$ DE = DF $，∴ $ Rt\triangle ADE \cong Rt\triangle ADF $(HL). ∴ $ AE = AF $. 又∵ $ \angle EAD = \angle FAD $，$ AK = AK $，∴ $ \triangle AEK \cong \triangle AFK $(SAS). ∴ $ EK = KF $，$ \angle AKE = \angle AKF = 90^\circ $. ∴ AD是线段EF的垂直平分线.

答案： 证明：设AD、EF的交点为K，
∵ AD平分$ \angle BAC $，$ DE \perp AB $，$ DF \perp AC $，
∴ $ DE = DF $.
∵ $ DE \perp AB $，$ DF \perp AC $，
∴ $ \angle AED = \angle AFD = 90^\circ $. 在 $ Rt\triangle ADE $ 和 $ Rt\triangle ADF $ 中，$ AD = AD $，$ DE = DF $，
∴ $ Rt\triangle ADE \cong Rt\triangle ADF (HL) $.
∴ $ AE = AF $. 又
∵ $ \angle EAD = \angle FAD $，$ AK = AK $，
∴ $ \triangle AEK \cong \triangle AFK $.
∴ $ EK = KF $，$ \angle AKE = \angle AKF = 90^\circ $.
∴ AD是线段EF的垂直平分线.

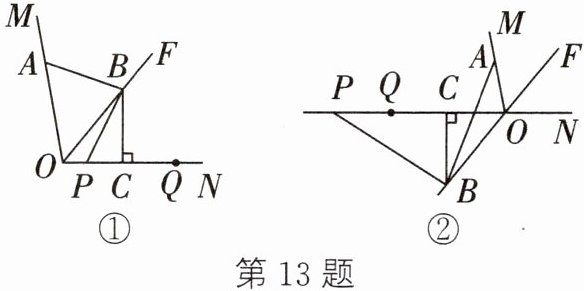
13. 如图,OF是$ ∠MON $的平分线,点A在射线OM上,P、Q是直线ON上的两动点,点Q在点P的右侧,且$ PQ = OA $,作线段OQ的垂直平分线,分别交直线OF、ON于点B、点C,连接AB、PB.
(1)如图①,请指出AB与PB的数量关系,并说明理由；
(2)如图②,当P、Q两点都在射线ON的反向延长线上时,线段AB、PB是否还存在(1)中的数量关系？若存在,请写出证明过程；若不存在,请说明理由.

答案：
解：
(1) $ AB = PB $. 理由：如图①中，连接BQ.
∵ BC垂直平分OQ，
∴ $ BO = BQ $.
∴ $ \angle BOQ = \angle BQO $.
∵ OF平分$ \angle MON $，
∴ $ \angle AOB = \angle BQO $.
∵ $ OA = PQ $，
∴ $ \triangle AOB \cong \triangle PQB (SAS) $.
∴ $ AB = PB $；
(2) 存在，理由：如图②中，连接BQ.
∵ BC垂直平分OQ，
∴ $ BO = BQ $.
∴ $ \angle BOQ = \angle BQO $.
∵ OF平分$ \angle MON $，$ \angle BOQ = \angle FON $，
∴ $ \angle AOF = \angle FON = \angle BQC $.
∴ $ \angle BQP = \angle AOB $.
∵ $ OA = PQ $，
∴ $ \triangle AOB \cong \triangle PQB (SAS) $.
∴ $ AB = PB $.
　　　　　　　　　　　　　　　　　　　　　　　　　　4