第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
1. 如图,将$\triangle ABC沿BC所在直线向右平移得到\triangle DEF$,则下列说法错误的是 (
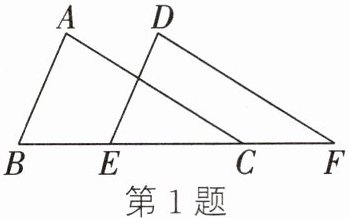
A. $\triangle ABC \cong \triangle DEF$
B. $AC \perp DE$
C. $AB // DE$
D. $BE = CF$
B
)
A. $\triangle ABC \cong \triangle DEF$
B. $AC \perp DE$
C. $AB // DE$
D. $BE = CF$
答案:
B
2. 如图,两个全等三角形重叠在一起,将其中的一个三角形沿着点$B到C的方向平移到\triangle DEF$的位置,$AB = 10$,$DO = 4$,平移距离为$6$,则阴影部分面积为______
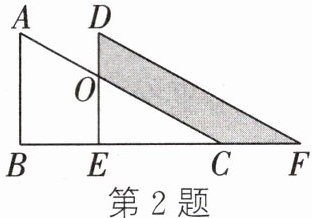
48
.
答案:
48
3. 如图,点$B$、$F$、$C$、$E$在一条直线上,$FB = CE$,$AC = DF$,请你从下列三个条件中选择一个合适的条件,使$AB // DE$成立,并说明理由.
供选择的条件:①$AB = DE$;②$\angle ACB = \angle DFE$;③$\angle A = \angle D$.
选择
供选择的条件:①$AB = DE$;②$\angle ACB = \angle DFE$;③$\angle A = \angle D$.
选择
①或②
:若选择①$AB=DE$,∵$FB=CE$,∴$FB+CF=CE+CF$.∴$BC=EF$.在$\triangle ABC$和$\triangle DEF$中,$\begin{cases}AB = DE\\AC = DF\\BC = EF\end{cases}$,∴$\triangle ABC≌\triangle DEF(SSS)$.∴$\angle B=\angle E$.∴$AB//ED$;若选择②$\angle ACB=\angle DFE$,∵$FB=CE$,∴$FB+CF=CE+CF$.∴$BC=EF$.在$\triangle ABC$和$\triangle DEF$中,$\begin{cases}AC = DF\\\angle ACB = \angle DFE\\BC = EF\end{cases}$,∴$\triangle ABC≌\triangle DEF(SAS)$.∴$\angle B=\angle E$.∴$AB//ED$.∵$FB=CE$,$AC=DF$,$\angle A=\angle D$,无法证明$\triangle ABC≌\triangle DEF$,进而不能得出$\angle B=\angle E$,∴不选择③.
答案:
选择①:AB=DE,
∵FB=CE,
∴FB+CF=CE+CF.
∴BC=EF.在△ABC和△DEF中,$\begin{cases}AB = DE\\AC = DF\\BC = EF\end{cases}$,
∴△ABC≌△DEF(SSS).
∴∠B=∠E.
∴AB//ED;选择②:∠ACB=∠DFE,
∵FB=CE,
∴FB+CF=CE+CF.
∴BC=EF.在△ABC和△DEF中,$\begin{cases}AC = DF\\∠ACB = ∠DFE\\BC = EF\end{cases}$,
∴△ABC≌△DEF(SAS).
∴∠B=∠E.
∴AB//ED.
∵FB=CE,AC=DF,∠A=∠D,无法证明△ABC≌△DEF,进而不能得出∠B=∠E,
∴不选择③.
∵FB=CE,
∴FB+CF=CE+CF.
∴BC=EF.在△ABC和△DEF中,$\begin{cases}AB = DE\\AC = DF\\BC = EF\end{cases}$,
∴△ABC≌△DEF(SSS).
∴∠B=∠E.
∴AB//ED;选择②:∠ACB=∠DFE,
∵FB=CE,
∴FB+CF=CE+CF.
∴BC=EF.在△ABC和△DEF中,$\begin{cases}AC = DF\\∠ACB = ∠DFE\\BC = EF\end{cases}$,
∴△ABC≌△DEF(SAS).
∴∠B=∠E.
∴AB//ED.
∵FB=CE,AC=DF,∠A=∠D,无法证明△ABC≌△DEF,进而不能得出∠B=∠E,
∴不选择③.
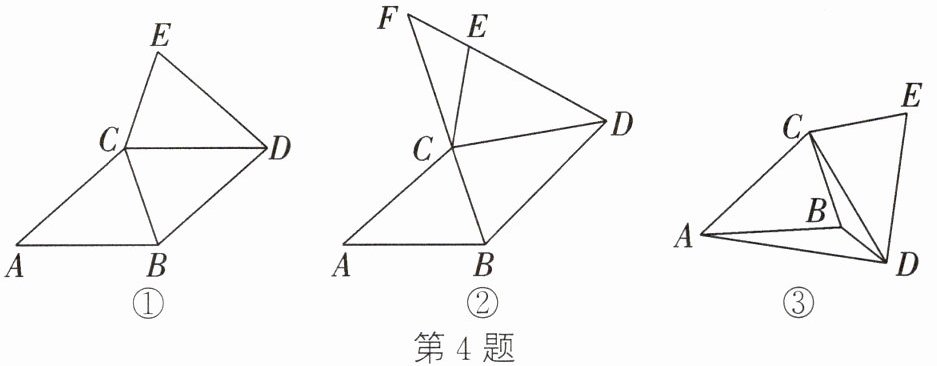
4. 已知:在等腰$\triangle ABC$中,$AB = AC$,$AB > BC$. 把$\triangle ABC绕点C逆时针旋转得到\triangle DEC$,其中点$D$、$E分别是点A$、$B$的对应点.
(1)如图①,若$\angle A = 40^{\circ}$,$CB平分\angle ACD$,求$\angle ACE$的度数;
(2)在$\triangle ABC$旋转过程中,若直线$BC$,$DE相交于点F$.
① 如图②,当点$D$、$E在直线BC$右侧时,若$\angle CFE = 45^{\circ}$,求$\angle ACE$的度数;
② 设$\angle CFE = \alpha(\alpha \neq 0)$,请直接用含$\alpha的式子表示\angle ACE$;
(3)如图③,若$\angle BAD = \angle BCD = 12^{\circ}$,请直接写出$\angle CDB$的度数.
(1)如图①,若$\angle A = 40^{\circ}$,$CB平分\angle ACD$,求$\angle ACE$的度数;
(2)在$\triangle ABC$旋转过程中,若直线$BC$,$DE相交于点F$.
① 如图②,当点$D$、$E在直线BC$右侧时,若$\angle CFE = 45^{\circ}$,求$\angle ACE$的度数;
② 设$\angle CFE = \alpha(\alpha \neq 0)$,请直接用含$\alpha的式子表示\angle ACE$;
(3)如图③,若$\angle BAD = \angle BCD = 12^{\circ}$,请直接写出$\angle CDB$的度数.

答案:
解:
(1)
∵AB=AC,∠A=40°,
∴∠ACB=∠ABC=$\frac{180^{\circ}-40^{\circ}}{2}$=70°.
∵把△ABC绕点C逆时针旋转得到△DEC,
∴∠ECD=∠ACB=70°.
∵CB平分∠ACD,
∴∠DCB=∠ACB=70°.
∴∠ACE=360°−∠ACB−∠DCB−∠ECD=360°−70°−70°−70°=150°;
(2)①设∠FCE=x°,
∵∠CFE=45°,
∴∠CED=45°+x°.
∵把△ABC绕点C逆时针旋转得到△DEC,
∴∠ABC=∠CED=45°+x°.
∵AB=AC,
∴∠ACB=∠ABC=45°+x°.
∴∠ACF=180°−∠ACB=135°−x°.
∴∠ACE=∠ACF+∠FCE=(135°−x°)+x°=135°; ②设∠FCE=β,当E在F右侧时,如图①,
∵∠CFE=α,
∴∠CED=α+β.
∵把△ABC绕点C逆时针旋转得到△DEC,
∴∠ABC=∠CED=α+β.
∵AB=AC,
∴∠ACB=∠ABC=α+β.
∴∠ACF=180°−∠ACB=180°−α−β.
∴∠ACE=∠ACF+∠FCE=(180°−α−β)+β=180°−α,即∠ACE=180°−α;当E在F左侧时,如图②,
∵∠E=180°−∠CFE−∠ECF=180°−α−β.
∴∠ACB=∠B=∠E=180°−α−β.
∴∠ACE=180°−∠ACB−∠ECF=180°−(180°−α−β)−β=α.综上所述,∠ACE为180°−α或α;
(3)在线段AD上取一点M,使AM=CB,连接BM,如图③,
∵∠BAD=∠BCD,AB=DC,
∴△BAM≌△DCB(SAS).
∴BM=DB,∠ABM=∠BDC.
∴∠BMD=∠BDM.
∵∠BMD=∠BAD+∠MBA,
∴∠ADB=∠BCD+∠BDC.设∠CDB=y°,
∵∠DAB=12°=∠BCD,
∴∠ADB=∠BCD+∠BDC=12°+y°.
∴∠ADC=∠ADB+∠CDB=12°+2y°.
∵CA=CD,
∴∠CAD=∠CDA=12°+2y°.
∴∠ACD=180°−∠CAD−∠CDA=180°−(12°+2y°)−(12°+2y°)=156°−4y°.
∵∠CAD=12°+2y°,∠BAD=12°,
∴∠CAB=∠CAD−∠BAD=2y°.
∵AB=AC,
∴∠ACB=∠ABC=$\frac{180^{\circ}-2y^{\circ}}{2}$=90°−y°.
∵∠ACD=∠ACB+∠BCD,
∴156°−4y°=90°−y°+12°,解得y=18,
∴∠CDB=18°.

解:
(1)
∵AB=AC,∠A=40°,
∴∠ACB=∠ABC=$\frac{180^{\circ}-40^{\circ}}{2}$=70°.
∵把△ABC绕点C逆时针旋转得到△DEC,
∴∠ECD=∠ACB=70°.
∵CB平分∠ACD,
∴∠DCB=∠ACB=70°.
∴∠ACE=360°−∠ACB−∠DCB−∠ECD=360°−70°−70°−70°=150°;
(2)①设∠FCE=x°,
∵∠CFE=45°,
∴∠CED=45°+x°.
∵把△ABC绕点C逆时针旋转得到△DEC,
∴∠ABC=∠CED=45°+x°.
∵AB=AC,
∴∠ACB=∠ABC=45°+x°.
∴∠ACF=180°−∠ACB=135°−x°.
∴∠ACE=∠ACF+∠FCE=(135°−x°)+x°=135°; ②设∠FCE=β,当E在F右侧时,如图①,
∵∠CFE=α,
∴∠CED=α+β.
∵把△ABC绕点C逆时针旋转得到△DEC,
∴∠ABC=∠CED=α+β.
∵AB=AC,
∴∠ACB=∠ABC=α+β.
∴∠ACF=180°−∠ACB=180°−α−β.
∴∠ACE=∠ACF+∠FCE=(180°−α−β)+β=180°−α,即∠ACE=180°−α;当E在F左侧时,如图②,
∵∠E=180°−∠CFE−∠ECF=180°−α−β.
∴∠ACB=∠B=∠E=180°−α−β.
∴∠ACE=180°−∠ACB−∠ECF=180°−(180°−α−β)−β=α.综上所述,∠ACE为180°−α或α;
(3)在线段AD上取一点M,使AM=CB,连接BM,如图③,
∵∠BAD=∠BCD,AB=DC,
∴△BAM≌△DCB(SAS).
∴BM=DB,∠ABM=∠BDC.
∴∠BMD=∠BDM.
∵∠BMD=∠BAD+∠MBA,
∴∠ADB=∠BCD+∠BDC.设∠CDB=y°,
∵∠DAB=12°=∠BCD,
∴∠ADB=∠BCD+∠BDC=12°+y°.
∴∠ADC=∠ADB+∠CDB=12°+2y°.
∵CA=CD,
∴∠CAD=∠CDA=12°+2y°.
∴∠ACD=180°−∠CAD−∠CDA=180°−(12°+2y°)−(12°+2y°)=156°−4y°.
∵∠CAD=12°+2y°,∠BAD=12°,
∴∠CAB=∠CAD−∠BAD=2y°.
∵AB=AC,
∴∠ACB=∠ABC=$\frac{180^{\circ}-2y^{\circ}}{2}$=90°−y°.
∵∠ACD=∠ACB+∠BCD,
∴156°−4y°=90°−y°+12°,解得y=18,
∴∠CDB=18°.

查看更多完整答案,请扫码查看


