《2025年轻松作业本八年级数学上册苏科版》

1. 如图,若$AD// BC$,$AD = BC$,$AC与BD相交于点O$,则图中的全等三角形一共有(B)

A. 3对
B. 4对
C. 5对
D. 6对

答案： B

2. 有一张三角形纸片$ABC$,已知$∠B = ∠C = α$,按如图两种方案用剪刀沿着箭头方向剪开,方案中两个阴影部分的三角形一定全等打“√”,不一定全等打“×”。则下列关于两种方案中两个阴影部分三角形全等情况的判断正确的是(D)

A. 方案一：√ 方案二：√
B. 方案一：× 方案二：×
C. 方案一：× 方案二：√
D. 方案一：√ 方案二：×

答案： D

3. 如图,$AB = AC$,$BD⊥AC于D$,$CE⊥AB于E$,$CE$、$BD交于点O$。则图中能够全等的直角三角形有4对。

答案： 4

4. (2025·淮安淮阴区模拟)如图,$AB// CD$,且$AB = BD$,点$E在BD$边上,连接$AE$,$∠C = ∠AEB$。求证：$BC = AE$。
证明：∵ $ AB // CD $，∴ $∠D = ∠ABE$。在 $ \triangle BDC $ 和 $ \triangle ABE $ 中，$ \left\{ \begin{array} { l } { \angle C = \angle AEB , } \\ { \angle D = \angle ABE , } \\ { BD = AB , } \end{array} \right. $ ∴ $ \triangle BDC \cong \triangle ABE$(AAS)。∴ $ BC = AE $。

答案： 证明：
∵ $ AB // CD $，
∴ $ \angle D = \angle ABE $。在 $ \triangle BDC $ 和 $ \triangle ABE $ 中，$ \left\{ \begin{array} { l } { \angle C = \angle AEB , } \\ { \angle D = \angle ABE , } \\ { B D = A B , } \end{array} \right. $
∴ $ \triangle B D C \cong \triangle A B E ( \mathrm { AAS } ) $。
∴ $ B C = A E $。

5. 如图,在四边形$ABCD$中,$AB// CD$,点$E是线段BD$上一点,连接$CE$。$∠ADB = ∠ECD$,$AD = EC$。求证：$BD = DC$。
证明：∵ $ A B // C D $，∴ $ \angle A B D = \angle B D C $。在 $ \triangle A B D $ 和 $ \triangle E D C $ 中，$ \left\{ \begin{array} { l } { \angle A B D = \angle B D C , } \\ { \angle A D B = \angle E C D , } \\ { A D = E C , } \end{array} \right. $ ∴ $ \triangle A B D \cong \triangle E D C $(AAS)。∴ $ B D = D C $。

答案： 证明：
∵ $ A B // C D $，
∴ $ \angle A B D = \angle B D C $。在 $ \triangle A B D $ 和 $ \triangle E D C $ 中，$ \left\{ \begin{array} { l } { \angle A B D = \angle B D C , } \\ { \angle A D B = \angle E C D , } \\ { A D = E C , } \end{array} \right. $
∴ $ \triangle A B D \cong \triangle E D C ( \mathrm { AAS } ) $。
∴ $ B D = D C $。

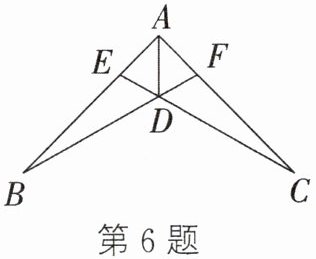
6. 如图,$AD平分∠BAC$,$AB = AC$,则此图中全等三角形有(C)

A. 2对
B. 3对
C. 4对
D. 5对

答案： C