《2025年轻松作业本八年级数学上册苏科版》

1. 如图,点E、F在BC上,$BE= CF$,$∠B= ∠C$,添加一个条件,不能证明$△ABF≌△DCE$的是(D)

A. $∠A= ∠D$
B. $∠AFB= ∠DEC$
C. $AB= DC$
D. $AF= DE$

答案： D

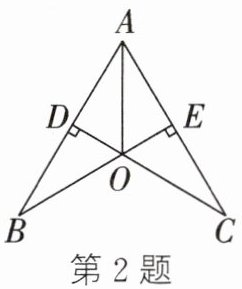
2. 如图,$CD⊥AB$于点D,$BE⊥AC$于点E,CD、BE交于点O,且AO平分$∠BAC$,则图中的全等三角形共有(D)

A. 1对
B. 2对
C. 3对
D. 4对

答案： D

3. 如图,$∠ABC= ∠DCB$,增加下列条件：①$AB= CD$；②$AC= DB$；③$∠A= ∠D$；④$∠ABO= ∠DCO$．能判定$△ABC≌△DCB$的是______①③④(填序号)．

答案： ①③④

4. 如图,D是AB上一点,DF交AC于点E,$FC// AB$,有下列结论：①若$AE= CE$,则$DE= FE$；②若$DE= FE$,则$AE= CE$；③若$BC= CF$,则$AD= CF$；④若$AD= CF$,则$DE= FE$．其中错误的有______③(填序号)．

答案： ③

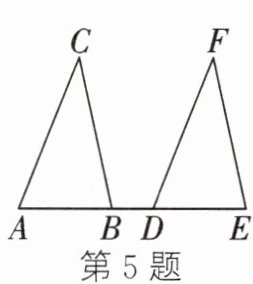
5. 如图,点A、B、D、E在同一条直线上,$AC// DF$,$BC// EF$,请添加一个条件______$ BC = EF $,使$△ACB≌△DFE$(填一个即可)．

答案： $ BC = EF $（答案不唯一）

6. 如图,$△ABC$的一个顶点A在$△DEC$的边DE上,AB交CD于点F,且$AC= EC$,$∠1= ∠2= ∠3$．试证明：$AB= DE$．
证明：$ \because ∠1 = ∠2 $，$ ∠AFD = ∠BFC $，$ \therefore ∠B = ∠D $。又 $ \because ∠2 = ∠3 $，$ \therefore ∠2 + ∠ACD = ∠3 + ∠ACD $，即 $ ∠BCA = ∠DCE $。在 $ △ABC $ 和 $ △EDC $ 中，$ \left\{ \begin{array} { l } { ∠B = ∠D, } \\ { ∠BCA = ∠DCE, } \\ { AC = EC, } \end{array} \right. $ $ \therefore △ABC ≌ △EDC (AAS) $。$ \therefore AB = ED $。

答案： 证明：$ \because ∠1 = ∠2 $，$ ∠AFD = ∠BFC $，$ \therefore ∠B = ∠D $。又 $ \because ∠2 = ∠3 $，$ \therefore ∠2 + ∠ACD = ∠3 + ∠ACD $，即 $ ∠BCA = ∠DCE $。在 $ △ABC $ 和 $ △EDC $ 中，$ \left\{ \begin{array} { l } { ∠B = ∠D, } \\ { ∠BCA = ∠DCE, } \\ { AC = EC, } \end{array} \right. $ $ \therefore △ABC ≌ △EDC (AAS) $。$ \therefore AB = ED $。

7. 如图,已知$EC= BF$,$∠A= ∠D$,现有下列6个条件：①$AC= DF$；②$∠B= ∠E$；③$∠ACB= ∠DFE$；④$AB// ED$；⑤$AB= ED$；⑥$DF// AC$．从中选取一个条件,以保证$△ABC≌△DEF$,则可选择的是(A)

A. ②③④⑥
B. ③④⑤⑥
C. ①③④⑥
D. ①②③④

答案： A