《2025年轻松作业本八年级数学上册苏科版》

1. 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法的根据是(D)

A. 两点之间线段最短
B. 长方形的对称性
C. 长方形的四个角都是直角
D. 三角形的稳定性

答案： D

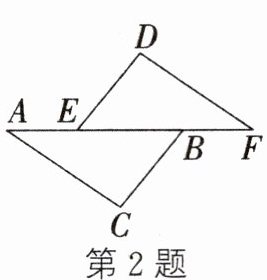
2. 如图,在△ABC和△FED中,AC= FD,BC= ED,要利用“SSS”来判定△ABC和△FED全等时,下面的4个条件中：①AE= FB；②AB= FE；③AE= BE；④BF= BE,可利用的是(A)

A. ①或②
B. ②或③
C. ①或③
D. ①或④

答案： A

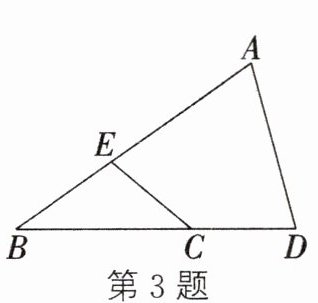
3. 如图,点C、E分别为△ABD的边BD、AB上的点,AE= AD,CE= CD,∠D= 75°,∠ECD= 140°,则∠B的度数为35°.

答案： 35

4. 如图,AB= AD,CB= CD,∠B= 30°,∠BAD= 46°,则∠ACD的度数是127°.

答案： $ 127^{\circ} $

5. 如图,△ABC中,AB= AC,AD是BC边上的中线,若∠BAC= 80°,则∠B= ______50°.

答案： $ 50^{\circ} $

6. (2024·内江)如图,点A、D、B、E在同一条直线上,AD= BE,AC= DF,BC= EF.
(1)求证：△ABC≌△DEF；
证明：∵AD= BE，∴AD+ BD= BE+ BD，即AB= DE。在△ABC和△DEF中，$\begin{cases} AB= DE, \\ AC= DF, \\ BC= EF, \end{cases}$∴△ABC≌△DEF(SSS)；
(2)若∠A= 55°,∠E= 45°,求∠F的度数.
解：∵∠A= 55°，∠E= 45°，由(1)可知：△ABC≌△DEF，∴∠A=∠FDE= 55°。∴∠F= 180°-(∠FDE+∠E)= 180°-(55°+ 45°)=80°。

答案：
(1) 证明：$ \because AD = BE $，$ \therefore AD + BD = BE + BD $，即 $ AB = DE $。在 $ \triangle ABC $ 和 $ \triangle DEF $ 中，$ \begin{cases} AB = DE, \\ AC = DF, \\ BC = EF, \end{cases} $ $ \therefore \triangle ABC \cong \triangle DEF $ (SSS)；
(2) 解：$ \because \angle A = 55^{\circ} $，$ \angle E = 45^{\circ} $，由
(1) 可知：$ \triangle ABC \cong \triangle DEF $，$ \therefore \angle A = \angle FDE = 55^{\circ} $。$ \therefore \angle F = 180^{\circ} - (\angle FDE + \angle E) = 180^{\circ} - (55^{\circ} + 45^{\circ}) = 80^{\circ} $。

7. 如图,AD= BC,AC= BD,则下列结论中,不正确的是(D)

A. OA= OB
B. OC= OD
C. ∠C= ∠D
D. ∠OAB= ∠DBA

答案： D