《2025年思维新观察八年级数学上册人教版湖北专版》

【典例】(2025·汉阳)【问题呈现】借助几何直观探究数量关系,是数形结合的常见方法,图 1,图 2 是用边长为 a,b 的两个正方形和边长为 a,b 的两个长方形拼成的一个大正方形,图 3 是用边长为 a,b 的四个长方形拼成的一个大正方形,利用图形可以推导出 a,b 的关系式为:
图 1:$a^{2}+b^{2}+2ab=(a+b)^{2}$;
图 2:$(a-b)^{2}=a^{2}+b^{2}-2ab$;
图 3:$(a-b)^{2}+4ab=(a+b)^{2}$.
【解决问题】
(1)直接写出结果:
①若 $ mn = 4,m^{2}+n^{2}= 25 $,则 $ (m + n)^{2}= $33;
②若 $ x + y = 6,x^{2}+y^{2}= 28 $,则 $ xy = $4.
(2)若 $ 3a + 2b = 8,ab = 2 $,求 a,b.
【拓展延伸】如图 4,以 $ Rt\triangle ABC $ 的直角边 AB,BC 为边作正方形 ABFG 和正方形 BCDE.若 $ \triangle ABC $ 的面积为 6, $ CF = 1 $,求 $ (AB + BC)^{2} $ 的值.

答案： 解：$a^{2}+b^{2}+2ab=(a+b)^{2}$
$(a-b)^{2}=a^{2}+b^{2}-2ab$
$(a-b)^{2}+4ab=(a+b)^{2}$
(1)①33；②4
(2)$(3a+2b)^{2}=64$，
$9a^{2}+4b^{2}=40$，
$\therefore (3a-2b)^{2}=16$，
$\therefore 3a-2b=4$或$-4$，
$\therefore a=2$，$b=1$或$a=\frac {2}{3}$，$b=3$；
【拓展延伸】设$BC=x$，$AB=y$，
$\frac {1}{2}xy=6$，$xy=12$，
$(y-x)^{2}=1$，$\therefore x^{2}+y^{2}-2xy=1$，
$x^{2}+y^{2}=25$，
$(x+y)^{2}=x^{2}+y^{2}+2xy=49$．

变式.(2025·江汉)如图,已知 E,F 分别是正方形 ABCD 的边 AD,DC 上的点,且 $ AE = 2 $, $ CF = 5 $,长方形 DEMF 的面积是 20,分别以 MF,DF 为边长作正方形 MFRN 和正方形 DHGF,直接写出阴影部分的面积.

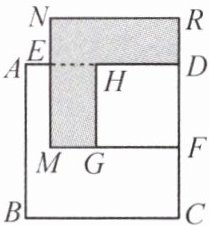
$3\sqrt{89}$

答案： 解：设$MF=x$，$DF=y$，
$x+2=y+5$，$\therefore x-y=3$，
$\therefore x^{2}+y^{2}-2xy=9$，
又$\because xy=20$，$\therefore x^{2}+y^{2}=49$，
$\therefore (x+y)^{2}=49+40=89$，
$\therefore S_{阴}=x^{2}-y^{2}=(x+y)(x-y)=3\sqrt {89}$．