第96页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
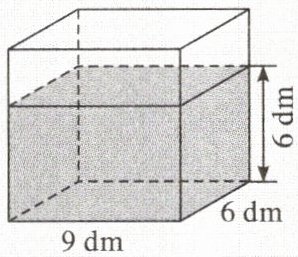
【对点训练1】有一个长方体鱼缸(如图),放进去一块珊瑚石(完全沉没),水面升高了$3 dm$,这块珊瑚石的体积是
162
$ dm^3$。
答案:
162 解析由题意得,这块珊瑚石的体
积为$9×6×3=162(dm^3)。$
积为$9×6×3=162(dm^3)。$
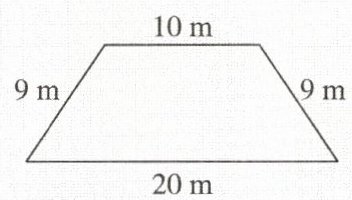
【例2】有一个梯形的篱笆,它的边长如图所示。因为另有他用,计划将它的形状改为一个正方形或者长是宽的$2$倍的长方形,要使围出的篱笆面积较大,应采用哪种围法?
[听课笔记]
_
_
_
_
名师点拨

[听课笔记]
_
_
_
_
名师点拨


答案:
解当篱笆围成正方形时,
因为正方形的边长为$\frac{10+9+20+9}{4}=12(m),$
所以正方形的面积为$12×12=144(m^2)。$
当篱笆围成长方形时,
设长方形的宽为x m,则长为2x m。
根据题意,得2(x+2x)=10+20+9+9。
解方程,得x=8,2x=8×2=16,
所以长方形的宽为8m,长为16m。
所以长方形的面积为$8×16=128(m^2)。$
因为144>128,所以围成正方形时面积较大。
因此,要使围出的篱笆面积较大,应围成正方形。
因为正方形的边长为$\frac{10+9+20+9}{4}=12(m),$
所以正方形的面积为$12×12=144(m^2)。$
当篱笆围成长方形时,
设长方形的宽为x m,则长为2x m。
根据题意,得2(x+2x)=10+20+9+9。
解方程,得x=8,2x=8×2=16,
所以长方形的宽为8m,长为16m。
所以长方形的面积为$8×16=128(m^2)。$
因为144>128,所以围成正方形时面积较大。
因此,要使围出的篱笆面积较大,应围成正方形。
【对点训练2】一个长方形的周长为$30 cm$,这个长方形的长减少$1 cm$,宽增加$2 cm$,就可以变成一个正方形。设长方形的长为$x cm$,可列方程是(
A.$x-1=(30-x)+2$
B.$x-1=(15-x)+2$
C.$x+1=(30-x)-2$
D.$x+1=(15-x)-2$
$\cdots\cdots\cdots\cdots\cdots\cdot\gt\gt\gt\gt\gt$ 作业·进阶演练 $\lt\lt\lt\lt\lt\cdot\cdots\cdots\cdots\cdots\cdots$
B
)A.$x-1=(30-x)+2$
B.$x-1=(15-x)+2$
C.$x+1=(30-x)-2$
D.$x+1=(15-x)-2$
$\cdots\cdots\cdots\cdots\cdots\cdot\gt\gt\gt\gt\gt$ 作业·进阶演练 $\lt\lt\lt\lt\lt\cdot\cdots\cdots\cdots\cdots\cdots$
答案:
B 解析由题意知,设长方形的长为
x cm,则宽为(30÷2-x)cm,
可列方程为x-1=(15-x)+2。
x cm,则宽为(30÷2-x)cm,
可列方程为x-1=(15-x)+2。
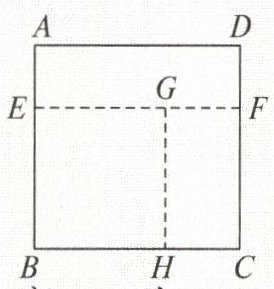
1.如图,某同学从一张正方形纸片$ABCD$上剪去一个宽$AE$为$5 cm$的长方形纸条$AEFD$,再从剩下的长方形纸片$BCFE$上剪去一个宽$CH$为$6 cm$的长方形纸条$CFGH$。若两次剪下的长方形纸条$AEFD$和$CFGH$的面积相等,则剪下的每一个长方形纸条的面积均为(
A.$30 cm^2$
B.$150 cm^2$
C.$160 cm^2$
D.$900 cm^2$
B
)
A.$30 cm^2$
B.$150 cm^2$
C.$160 cm^2$
D.$900 cm^2$
答案:
1.B 解析设正方形ABCD的边长为x cm,则长方
形AEFD的面积为$5x cm^2,$长方形CFGH的面积为
$6(x-5)cm^2。$
因为两次剪下的长方形纸条AEFD和CFGH的面
积相等,所以5x=6(x-5),解得x=30,
所以$5×30=150(cm^2),$
故剪下的每一个长方形纸条的面积均为$150cm^2。$
形AEFD的面积为$5x cm^2,$长方形CFGH的面积为
$6(x-5)cm^2。$
因为两次剪下的长方形纸条AEFD和CFGH的面
积相等,所以5x=6(x-5),解得x=30,
所以$5×30=150(cm^2),$
故剪下的每一个长方形纸条的面积均为$150cm^2。$
2.如图,相同的$8$块小长方形地砖拼成一个大长方形,每块小长方形地砖长是(
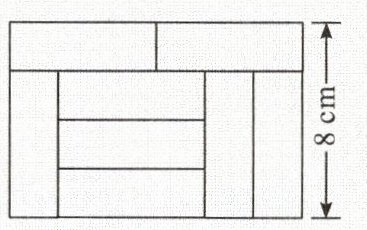
A.$2 cm$
B.$\frac{5}{2} cm$
C.$6 cm$
D.$4 cm$
C
)
A.$2 cm$
B.$\frac{5}{2} cm$
C.$6 cm$
D.$4 cm$
答案:
2.C
3.一种牙膏出口处直径为$5 mm$,小明每次刷牙都挤出$1 cm$长的牙膏,这样一支牙膏可以用$36$次。该品牌牙膏推出新包装,只是将出口处直径改为$6 mm$,小明还是按习惯每次挤出$1 cm$长的牙膏,这样一支牙膏能用
25
次。
答案:
3.25 解析由题意知,牙膏的体积为$\pi × (\frac{5}{2})^2 ×$
$10×36=2250\pi(mm^3),$所以能用的次数为$2250\pi ÷$
$[\pi × (\frac{6}{2})^2 × 10]=25。$
$10×36=2250\pi(mm^3),$所以能用的次数为$2250\pi ÷$
$[\pi × (\frac{6}{2})^2 × 10]=25。$
查看更多完整答案,请扫码查看


