第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
5. 在直线l上顺次取A,B,C三点,使得AB = 5 cm,BC = 7 cm。如果点O是线段AC的中点,那么线段OB的长度是
1
cm。
答案:
5.1
6. 已知线段a,b,c,求作:线段m,使m = a - b + c。
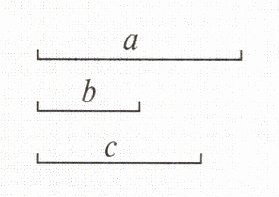

答案:
6.解 作法不唯一。举例:
(1)画射线AM;
(2)在射线AM上依次截取线段AB=a,BC=c;
(3)在线段AC上截取AD=b。则线段DC就是所要求作的线段m。
(1)画射线AM;
(2)在射线AM上依次截取线段AB=a,BC=c;
(3)在线段AC上截取AD=b。则线段DC就是所要求作的线段m。
7. 阳光大课间活动时,小明、小亮、小刚三名同学站在操场上的同一条直线上做广播体操,若小明与小亮相距3 m,小亮与小刚相距1 m,则小明与小刚的距离是(
A.4 m
B.2 m
C.1 m或3 m
D.2 m或4 m
D
)A.4 m
B.2 m
C.1 m或3 m
D.2 m或4 m
答案:
7.D
8. 已知点C是直线AB上的一点,点D是线段BC的中点,若AB = 10 cm,AC = 2 cm,则BD的长为
6或4
cm。
答案:
8.6或4 解析 ①如图1,点C在线段AB上时,
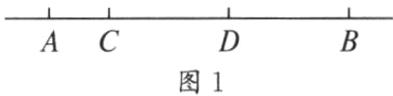
因为AB=10cm,AC=2cm,所以BC=AB−AC=10−2=8(cm)。因为D是线段BC的中点,所以BD=$\frac{1}{2}$BC=4cm。
②如图2,点C在线段BA的延长线上时,
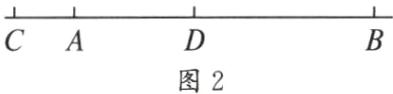
因为AB=10cm,AC=2cm,所以BC=AB+AC=10+2=12(cm)。因为D是线段BC的中点,所以BD=$\frac{1}{2}$BC=6cm。
综上所述,线段BD的长为4cm或6cm。
8.6或4 解析 ①如图1,点C在线段AB上时,

因为AB=10cm,AC=2cm,所以BC=AB−AC=10−2=8(cm)。因为D是线段BC的中点,所以BD=$\frac{1}{2}$BC=4cm。
②如图2,点C在线段BA的延长线上时,

因为AB=10cm,AC=2cm,所以BC=AB+AC=10+2=12(cm)。因为D是线段BC的中点,所以BD=$\frac{1}{2}$BC=6cm。
综上所述,线段BD的长为4cm或6cm。
9. 如图,已知线段AB上有两点C,D,且AC = BD,点M,N分别是线段AC和AD的中点,若线段AB = a cm,AC = BD = b cm,且a,b满足$(a - 20)^2 + |\frac{b}{2} - 8| = 0$。

(1)求线段AB,AC的长度;
(2)求线段MN的长度。

(1)求线段AB,AC的长度;
(2)求线段MN的长度。
答案:
9.解
(1)由题意可知$(a - 20)^2 = 0$,$\frac{b}{2} - 8 = 0$,解得a=20,b=16,所以AB=20cm,AC=16cm。
(2)因为BD=AC=16cm,所以AD=AB−BD=4cm。又因为M,N分别是线段AC,AD的中点,所以AM=8cm,AN=2cm。所以MN=AM−AN=6cm。
(1)由题意可知$(a - 20)^2 = 0$,$\frac{b}{2} - 8 = 0$,解得a=20,b=16,所以AB=20cm,AC=16cm。
(2)因为BD=AC=16cm,所以AD=AB−BD=4cm。又因为M,N分别是线段AC,AD的中点,所以AM=8cm,AN=2cm。所以MN=AM−AN=6cm。
知识点1 角的定义和表示方法
1. 角的定义
(1) 静态定义:由两条具有公共端点的
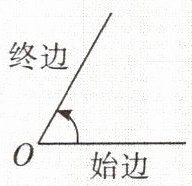
(2) 动态定义:角也可以看成由一条射线绕着它的端点
2. 角的表示
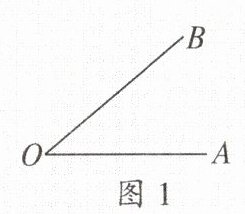
(1) 用一个大写英文字母表示,如图1,可记作∠O。用这种方法表示角的前提是以一个点作顶点的角只有
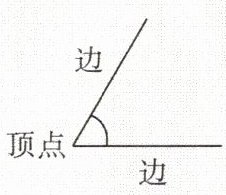
(2) 用数字来表示,用这种方法表示角时,要在靠近顶点处加上
(3) 用
(4) 用
1. 角的定义
(1) 静态定义:由两条具有公共端点的
射线
组成的图形,这个公共端点是角的顶点
,这两条射线是角的边(如图)。(2) 动态定义:角也可以看成由一条射线绕着它的端点
旋转
而成的(如图)。2. 角的表示
(1) 用一个大写英文字母表示,如图1,可记作∠O。用这种方法表示角的前提是以一个点作顶点的角只有
1
个,否则不能用这种方法表示。
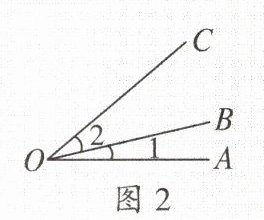
(2) 用数字来表示,用这种方法表示角时,要在靠近顶点处加上
弧
线,注上阿拉伯数字1,2,3等。如图2,∠AOB记作∠1,∠BOC记作∠2。
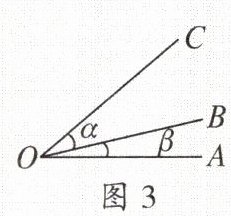
(3) 用
小写
希腊字母来表示,用这种方法表示角时,要在靠近顶点处加上弧线,注上小写希腊字母α,β,γ等。如图3,∠AOB记作∠β,∠BOC记作∠α。(4) 用
3
个大写英文字母表示,如图1,记作∠AOB或∠BOA,其中,O是角的顶点,写在中间;A和B分别是角的两边上的一点,写在两边,可以交换位置。


答案:
1.
(1)射线 顶点
(2)旋转 2.
(1)1
(2)弧
(3)小写
(4)3
(1)射线 顶点
(2)旋转 2.
(1)1
(2)弧
(3)小写
(4)3
查看更多完整答案,请扫码查看


