《2025年家庭作业七年级数学上册北师大版》

知识点 代数式的值
用具体数值代替代数式中的字
母，就可以求出代数式的值。

答案： 数值

【例1】当$x = 0,x = \frac{1}{2},x = 2$时，分别求代数式$2x^{2}-x + 1$的值。
[听课笔记]解 当$x=0$时，$2x^{2}-x + 1 = 2×0^{2}-0 + 1 = 1$。当$x=\frac{1}{2}$时，$2x^{2}-x + 1 = 2×(\frac{1}{2})^{2}-\frac{1}{2}+1 = 2×\frac{1}{4}-\frac{1}{2}+1 = 1$。 当$x = 2$时，$2x^{2}-x + 1 = 2×2^{2}-2 + 1 = 2×4 - 2 + 1 = 7$。
☑名师点拨 求代数式的值的方法
(1)用数值代替代数式中的字母，简称“代入”。
(2)按照代数式中的运算关系计算得出结果。

答案： 解 当$x=0$时，$2x^{2}-x + 1 = 2×0^{2}-0 + 1 = 1$。
当$x=\frac{1}{2}$时，$2x^{2}-x + 1 = 2×(\frac{1}{2})^{2}-\frac{1}{2}+1 = 2×\frac{1}{4}-\frac{1}{2}+1 = 1$。 当$x = 2$时，$2x^{2}-x + 1 = 2×2^{2}-2 + 1 = 2×4 - 2 + 1 = 7$。

【对点训练1】当$a = 2,b = 1,c = 3$时，求下列各代数式的值：
(1)$b^{2}-4ac$；(2)$a^{2}+b^{2}+c^{2}+2ab + 2bc + 2ac$；(3)$(a + b + c)^{2}$。

答案：
(1)当$a = 2,b = 1,c = 3$时，$b^{2}-4ac = 1^{2}-4×2×3 = 1 - 24 = -23$；
(2)当$a = 2,b = 1,c = 3$时，$a^{2}+b^{2}+c^{2}+2ab + 2bc + 2ac = 2^{2}+1^{2}+3^{2}+2×2×1 + 2×1×3 + 2×2×3 = 4 + 1 + 9 + 4 + 6 + 12 = 36$；
(3)当$a = 2,b = 1,c = 3$时，$(a + b + c)^{2}=(2 + 1 + 3)^{2}=36$。

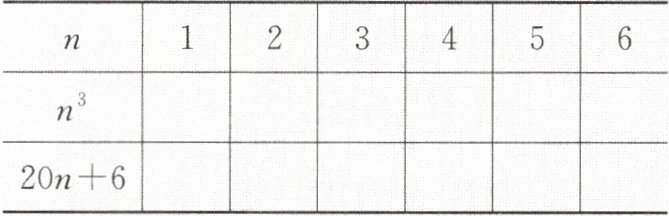
【例2】(1)填写下表，求出当$n = 1,2,3,4,5,6$时，两个代数式的值；

(2)估计一下随着$n$的值逐渐变大，哪个代数式的值会首先超过600？
[听课笔记]解 (1)填表如下：
$n$ 1 2 3 4 5 6
$n^{3}$ 1 8 27 64 125 216
$20n + 6$ 26 46 66 86 106 126(2)由(1)中求出的$n^{3}$，$20n + 6$的值，观察两个代数式的变化规律，可以发现，随着$n$的值逐渐变大，$n^{3}$比$20n + 6$的值增加得快，且当$n = 5$时，$n^{3}$开始大于$20n + 6$，故$n^{3}$的值会首先超过$600$。
☑名师点拨 解决该类问题时，通常先把字母所取的部分具体数值代入代数式进行求值，再观察字母的取值变化与代数式的值的变化之间的联系，最后根据代数式值的变化趋势进行预测，推断代数式所反映的规律。

答案：
(1)填表如下：
$n$ 1 2 3 4 5 6
$n^{3}$ 1 8 27 64 125 216
$20n + 6$ 26 46 66 86 106 126
(2)由
(1)中求出的$n^{3}$，$20n + 6$的值，观察两个代数式的变化规律，可以发现，随着$n$的值逐渐变大，$n^{3}$比$20n + 6$的值增加得快，且当$n = 5$时，$n^{3}$开始大于$20n + 6$，故$n^{3}$的值会首先超过$600$。