第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
4.甲、乙两名同学做游戏,其中甲同学站在第2层,乙同学从第2层开始做上下楼运动,他把自己上下楼的层数记录了下来:$+ 2$,$- 1$,$+ 3$,$- 2$,$+ 1$,$- 2$(注:负号表示相对于前一次为下楼,正号表示相对于前一次为上楼)。那么请你帮助甲同学算一下,乙同学最后在第
3
层。
答案:
4.3 解析2−1+3−2+1−2=1(层),2+1=3(层),故乙同学最后在第3层。
5.计算:
(1)$- 3\frac{1}{3} + ( - \frac{1}{2}) - ( - \frac{1}{3}) + 1\frac{1}{2}$;
(2)$( - 5.3) + | - 2.5| + ( - 3.2) - ( + 4.8)$。
(1)$- 3\frac{1}{3} + ( - \frac{1}{2}) - ( - \frac{1}{3}) + 1\frac{1}{2}$;
(2)$( - 5.3) + | - 2.5| + ( - 3.2) - ( + 4.8)$。
答案:
5.解$(1)−3\frac{1}{3}+(−\frac{1}{2})−(−\frac{1}{3})+1\frac{1}{2}=(−3\frac{1}{3}+\frac{1}{3})+(−\frac{1}{2}+1\frac{1}{2})=−3+1=−2;$
(2)(−5.3)+∣−2.5∣+(−3.2)−(+4.8)=−5.3+2.5−3.2−4.8=2.5−(5.3+3.2+4.8)=2.5−13.3=−10.8。
(2)(−5.3)+∣−2.5∣+(−3.2)−(+4.8)=−5.3+2.5−3.2−4.8=2.5−(5.3+3.2+4.8)=2.5−13.3=−10.8。
6.计算$- 21\frac{2}{5} + 3\frac{1}{6} + \frac{2}{5} - \frac{1}{6}$,最适当的方法是(
A.$- 21\frac{2}{5} + 3\frac{1}{6} + \frac{2}{5} + ( - \frac{1}{6})$
B.$( - 21\frac{2}{5} + 3\frac{1}{6}) + ( \frac{2}{5} - \frac{1}{6})$
C.$( - 21\frac{2}{5} - \frac{1}{6}) + ( 3\frac{1}{6} + \frac{2}{5})$
D.$( - 21\frac{2}{5} + \frac{2}{5}) + ( 3\frac{1}{6} - \frac{1}{6})$
D
)A.$- 21\frac{2}{5} + 3\frac{1}{6} + \frac{2}{5} + ( - \frac{1}{6})$
B.$( - 21\frac{2}{5} + 3\frac{1}{6}) + ( \frac{2}{5} - \frac{1}{6})$
C.$( - 21\frac{2}{5} - \frac{1}{6}) + ( 3\frac{1}{6} + \frac{2}{5})$
D.$( - 21\frac{2}{5} + \frac{2}{5}) + ( 3\frac{1}{6} - \frac{1}{6})$
答案:
6.D
7.如图,小李在某运动APP中,设定了每天的步数目标为8000步,该APP用目标线上方或下方的柱状图表示每天超过或少于目标数的步数。如3日,小李少于目标数的步数500步,则从2日到5日这四天中小李一共走的步数为(
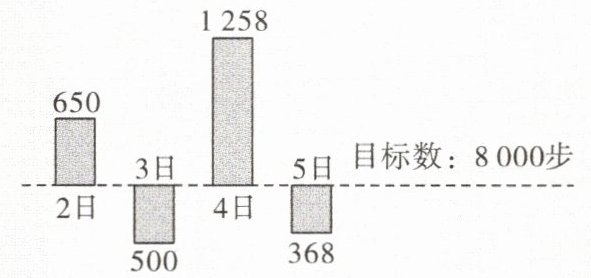
A.33040步
B.34776步
C.32040步
D.32000步
A
)
A.33040步
B.34776步
C.32040步
D.32000步
答案:
7.A
8.甲城市与乙城市的时差为两城市同一时刻时数之差,如北京时间为$8:00$时,东京时间为$9:00$,巴黎时间为$1:00$,那么东京与北京的时差为1小时,巴黎与北京的时差为$-7$小时。李教授搭乘北京早上$8:00$的飞机经过10小时到达巴黎,那么李教授到达巴黎时,巴黎时间为
11:00
。
答案:
8.11:00 解析由题意得8+10−7=18−7=11(时),
故李教授到达巴黎时,巴黎时间为11:00。
故李教授到达巴黎时,巴黎时间为11:00。
9.某汽车厂计划上半年内每月生产汽车20辆,由于实行轮休,每月上班人数不一定相等,实际每月生产量与计划量相比情况如下表(增加为正,减少为负)。

(1)实际生产量最多的一个月比实际生产量最少的一个月多生产多少辆?
(2)半年内实际总生产量比计划量多了还是少了,多或少了多少?半年内实际总生产量是多少?

(1)实际生产量最多的一个月比实际生产量最少的一个月多生产多少辆?
(2)半年内实际总生产量比计划量多了还是少了,多或少了多少?半年内实际总生产量是多少?
答案:
9.解
(1)实际生产量最多、最少的月份分别是4月和6月,4−(−5)=9(辆),
即实际生产量最多的一个月比实际生产量最少的一个月多生产9辆。
(2)这6个月增加和减少量的和是3+(−2)+(−1)+4+2+(−5)=1(辆),因此实际总生产量比计划多了,多生产了1辆,这半年内实际总生产量是6×20+1=121(辆)。
(1)实际生产量最多、最少的月份分别是4月和6月,4−(−5)=9(辆),
即实际生产量最多的一个月比实际生产量最少的一个月多生产9辆。
(2)这6个月增加和减少量的和是3+(−2)+(−1)+4+2+(−5)=1(辆),因此实际总生产量比计划多了,多生产了1辆,这半年内实际总生产量是6×20+1=121(辆)。
查看更多完整答案,请扫码查看


