《2025年家庭作业七年级数学上册北师大版》

【对点训练1】一个多项式加 $4x^{3} - x^{2} + 5$ 得 $3x^{4} - 4x^{3} - x^{2} + x - 8$，求这个多项式。

答案： 解$(3x^{4}-4x^{3}-x^{2}+x - 8)-$
$(4x^{3}-x^{2}+5)=3x^{4}-4x^{3}-x^{2}+x - 8 - 4x^{3}+x^{2}-5=$
$3x^{4}-8x^{3}+x - 13，$故所求多项式为$3x^{4}-8x^{3}+x - 13。$

【例2】某商店有一种商品，每件成本为 $a$ 元，原来按成本增加 $b$ 元定出售价，售出40件后，由于库存积压，调整为按售价的80%出售，又销售了60件。
(1)销售100件这种商品的总金额为多少元？
(2)销售100件这种商品共盈利多少元？
[听课笔记]
________________________
________________________
________________________
________________________
________________________
________________________
________________________
________________________
________________________
名师点拨 运用整式的加减运算解决实际问题的一般步骤：(1)列式，找准数量关系，正确添加括号，列出算式；(2)计算，去括号，合并同类项，得出结果。

答案： 解
(1)根据题意得40(a + b)+60(a + b)×
80%=88a + 88b(元)，则销售100件这种商品的总金额
为(88a + 88b)元。
(2)根据题意得88a + 88b - 100a=-12a + 88b(元)，
则销售100件这种商品共盈利(-12a + 88b)元。

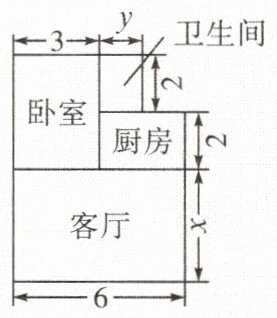
【对点训练2】小华购买了一套商品房，平面结构如图所示。他准备将地面铺上地砖，根据图中的数据(单位：m)，解答下列问题：
(1)用含 $x$，$y$ 的式子表示地面总面积。
(2)如果 $x = 4m$，$y = 1.5m$，铺 $1m^{2}$ 地砖的平均费用为80元，那么铺地砖的总费用为多少元？

答案： 解
(1)地面总面积:3×4 + 2y + 3×
$2 + 6x=6x + 2y + 18(m^{2})。$
(2)当x = 4m，y = 1.5m时，6x + 2y + 18=6×4+
$2×1.5 + 18=45(m^{2})。$80×45=3600(元)。
所以铺地砖的总费用为3600元。