第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
2. 几何体是由曲面或平面围成的。下列几何体面数最少的是(

A B C D
C
)
A B C D
答案:
2.C
3. 观察下图,左边的图形绕给定的直线旋转一周后形成的几何体是(

A B C D
D
)
A B C D
答案:
3.D
4. 图形是由点、线、面构成的,点动成线,线动成面,面动成体,下列场景中可以反映“点动成线”的是(
A.流星划过夜空
B.打开折扇
C.汽车雨刷的转动
D.旋转门的旋转
A
)A.流星划过夜空
B.打开折扇
C.汽车雨刷的转动
D.旋转门的旋转
答案:
4.A
5. 某酒店大堂的旋转门内部由四块宽2m、长3m的长方形玻璃隔板组成。
(1)每扇旋转门旋转一周,形成的几何体是
(2)求每扇旋转门旋转一周形成的几何体的体积(结果保留$\pi$)。
(1)每扇旋转门旋转一周,形成的几何体是
圆柱
,这体现了面
动成体;(2)求每扇旋转门旋转一周形成的几何体的体积(结果保留$\pi$)。
答案:
5.解
(1)圆柱 面
$(2)\pi × 2^{2} × 3 = 12\pi(m^{3}),$
故每扇旋转门旋转一周形成的几何体的体积为$12\pi m^{3}。$
(1)圆柱 面
$(2)\pi × 2^{2} × 3 = 12\pi(m^{3}),$
故每扇旋转门旋转一周形成的几何体的体积为$12\pi m^{3}。$
6. 如果我们将一枚硬币竖立在桌面,击打一侧使其快速旋转,就会看到一个“球”,这个过程蕴含的数学原理是(
A.点动成线
B.线动成面
C.面动成体
D.什么都不能说明
C
)A.点动成线
B.线动成面
C.面动成体
D.什么都不能说明
答案:
6.C
7. ①一条直线和一个曲面相交,可能得到两个交点;②一个平面和一条曲线相交,可能得到两个交点;③两个平面相交,可能得到一条曲线;④一个平面与一个曲面相交,可能得到一条直线。以上说法中错误的个数为(
A.0
B.1
C.2
D.3
B
)A.0
B.1
C.2
D.3
答案:
7.B
8. 小军和小红分别将直角梯形的上底和下底绕图中虚线旋转一周,得到甲、乙两个几何体。小军:“我们旋转的平面图形是完全一样的,所以旋转后得到的两个几何体的体积相等。”
小红:“我不同意你的看法,我认为甲、乙两个几何体的体积不相等。”
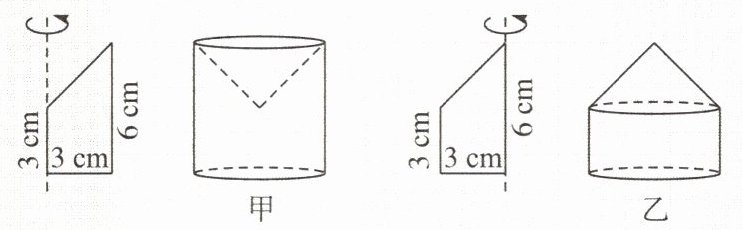
(1)你同意
(2)甲、乙两个几何体的体积比是多少?
小红:“我不同意你的看法,我认为甲、乙两个几何体的体积不相等。”

(1)你同意
小红
的说法。(2)甲、乙两个几何体的体积比是多少?
答案:
8.解
(1)小红
(2)甲的体积$:\pi × 3^{2} × 6 - \frac{1}{3} × \pi × 3^{2} × (6 - 3)=$
$54\pi - 9\pi = 45\pi(cm^{3}),$
乙的体积$:\pi × 3^{2} × 3 + \frac{1}{3} × \pi × 3^{2} × (6 - 3)= 27\pi +$
$9\pi = 36\pi(cm^{3}),$
$45\pi:36\pi = 5:4。$
故甲、乙两个几何体的体积比是5:4。
(1)小红
(2)甲的体积$:\pi × 3^{2} × 6 - \frac{1}{3} × \pi × 3^{2} × (6 - 3)=$
$54\pi - 9\pi = 45\pi(cm^{3}),$
乙的体积$:\pi × 3^{2} × 3 + \frac{1}{3} × \pi × 3^{2} × (6 - 3)= 27\pi +$
$9\pi = 36\pi(cm^{3}),$
$45\pi:36\pi = 5:4。$
故甲、乙两个几何体的体积比是5:4。
查看更多完整答案,请扫码查看


