《2025年家庭作业七年级数学上册北师大版》

【对点训练2】圆心角为$120^{\circ}$，半径长为6 cm的扇形面积是12π$cm^{2}$。

答案： 1. 12π 解析 由题意得，扇形的面积为$\frac{1}{3}$×π×6²=12π(cm²)。

1. 下列说法：在一个平面内，①经过点P的圆有无数个；②以点P为圆心的圆有无数个；③半径为3 cm且经过点P的圆有无数个；④以点P为圆心、3 cm为半径的圆有无数个。其中错误的有(A)

A.1个
B.2个
C.3个
D.4个

答案： 1. A

2. 若一个多边形从一个顶点最多能引出6条对角线，则这个多边形是(C)

A.六边形
B.八边形
C.九边形
D.十边形

答案： 2. C 解析 设多边形边数为n，由题意得n - 3=6，解得n=9。故选C。

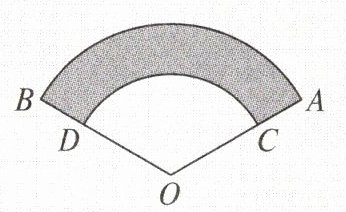
3. 如图，某小区要对一扇形空地进行绿化，准备在小扇形(空白部分)内种花，在其余区域(阴影部分)内种草，测得$\angle AOB = 120^{\circ}$，$OA = 15m$，$OC = 10m$，则种草区域的面积为(B)


A.$\frac{25\pi}{3}m^{2}$
B.$\frac{125\pi}{3}m^{2}$
C.$\frac{250\pi}{3}m^{2}$
D.$\frac{125}{3}m^{2}$

答案： 3. B 解析 由题意得S_{阴影}=$\frac{1}{3}$×π×15² - $\frac{1}{3}$×π×10²=$\frac{125π}{3}$(m²)。故选B。

4. 在梯形、正方形、直角三角形中，正多边形是正方形。

答案： 4. 正方形

5. 已知时钟的时针长6 cm，从7时到11时，时针扫过的面积是12π$cm^{2}$(保留$\pi$)。

答案： 5. 12π

6. 要使得一个多边形具有稳定性，从多边形一条边上的一点(不是顶点)出发，连接各个顶点转化得到2024个三角形，则这个多边形的边数为(D)

A.2022
B.2023
C.2024
D.2025

答案： 6. D 解析 设多边形的边数为n，由题意得n - 1=2024，解得n=2025，故选D。

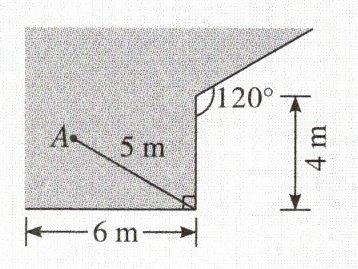
7. 如图，一根5 m长的绳子，一端拴在围墙墙角的柱子上，另一端拴着一只小羊A(羊只能在草地上活动，草地为阴影部分)，那么小羊A在草地上的最大活动区域面积是$\frac{77}{12}$π$m^{2}$。

答案：
7. $\frac{77}{12}$π 解析 如图，小羊A在草地上的最大活动区域面积是$\frac{1}{4}$×π×5² + $\frac{1}{6}$×π×1²=$\frac{77}{12}$π(m²)。
　　　　　　　　　　　　　

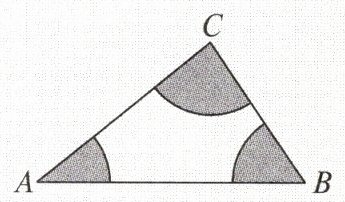
8. 如图，三角形广场ABC的三个角处各建一个半径相等的扇形草坪，扇形草坪的半径长为20 m，求草坪的总面积($\pi$取3.14)。

答案： 8. 解 把题图中三个扇形组合在一块，可知组成了一个半圆，所以草坪的总面积为$\frac{1}{2}$×π×20²=200π=628(m²)。