《2025年家庭作业七年级数学上册北师大版》

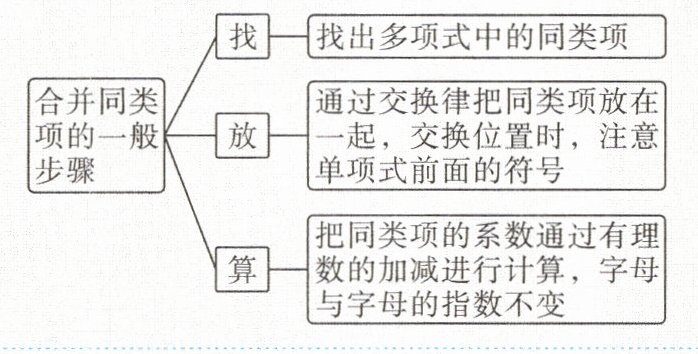
【例2】将下列各式合并同类项。
(1)$-x - x - x$；
(2)$2x^{2}y - 3x^{2}y + 5x^{2}y$；
(3)$2a^{2} - 3ab + 4b^{2} - 5ab - 6b^{2}$；
(4)$-ab^{3} + 2a^{3}b + 3ab^{3} - 4a^{3}b$。
[听课笔记]
________
名师点拨

答案： 解
(1)$-x - x - x = (-1 - 1 - 1)x = -3x$；
(2)$2x^{2}y - 3x^{2}y + 5x^{2}y = (2 - 3 + 5)x^{2}y = 4x^{2}y$；
(3)$2a^{2} - 3ab + 4b^{2} - 5ab - 6b^{2} = 2a^{2} + (4 - 6)b^{2} + (-3 - 5)ab = 2a^{2} - 2b^{2} - 8ab$；
(4)$-ab^{3} + 2a^{3}b + 3ab^{3} - 4a^{3}b = (-1 + 3)ab^{3} + (2 - 4)a^{3}b = 2ab^{3} - 2a^{3}b$。

【对点训练2】下列各组合并同类项结果正确的是(D)

A.$3a + 2b = 5ab$
B.$5y^{2} - 2y^{2} = 3$
C.$2m + 2m = 4m^{2}$
D.$a^{2}b - ba^{2} = 0$

答案： D 解析A中，$3a$与$2b$不是同类项，因而它们不能合并；B中，$5y^{2} - 2y^{2} = 3y^{2}$；C中，$2m + 2m = 4m$；D中，$a^{2}b - ba^{2} = a^{2}b - a^{2}b = 0$，只有D项结果正确，故选D。

【例3】先化简，再求值：$2a^{2}b - 2ab + 3 - 3a^{2}b + 4ab$，其中$a = -2$，$b = \frac{1}{2}$。
[听课笔记]
________
名师点拨
多项式化简求值时，一般先化简，即先合并同类项，再代入值计算结果。在算式中代入负数时，要注意添加括号。

答案： 解$2a^{2}b - 2ab + 3 - 3a^{2}b + 4ab = (2 - 3)a^{2}b + (-2 + 4)ab + 3 = -a^{2}b + 2ab + 3$。将$a = -2$，$b = \frac{1}{2}$代入，得原式$= -(-2)^{2} × \frac{1}{2} + 2 × (-2) × \frac{1}{2} + 3 = -1$。

【对点训练3】求多项式的值：$3x^{2} + 4x - 2x^{2} - x + x^{2} - 3x - 1$，其中$x = -3$。

答案： 解 原式$= (3x^{2} - 2x^{2} + x^{2}) + (4x - x - 3x) - 1 = (3 - 2 + 1)x^{2} + (4 - 1 - 3)x - 1 = 2x^{2} - 1$。当$x = -3$时，原式$= 2 × (-3)^{2} - 1 = 18 - 1 = 17$。

1. 下列说法正确的是(C)

A.$3x^{2}$与$ax^{2}$是同类项
B.$6$与$x$是同类项
C.$3x^{3}y^{2}$与$-3x^{3}y^{2}$是同类项
D.$2x^{2}y^{3}$与$-2x^{3}y^{2}$是同类项

答案： 1 C