第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
【对点训练1】把下列各式写成乘方的形式:
(1)$(+\frac{2}{5})× (+\frac{2}{5})× (+\frac{2}{5})× (+\frac{2}{5})$;
(2)$(-3.7)× (-3.7)× (-3.7)× (-3.7)× 5× 5$。
(1)$(+\frac{2}{5})× (+\frac{2}{5})× (+\frac{2}{5})× (+\frac{2}{5})$;
(2)$(-3.7)× (-3.7)× (-3.7)× (-3.7)× 5× 5$。
答案:
1.解
(1)$\left( + \frac{2}{5} \right) × \left( + \frac{2}{5} \right) × \left( + \frac{2}{5} \right) × \left( + \frac{2}{5} \right) = \left( + \frac{2}{5} \right)^{4} = \left( \frac{2}{5} \right)^{4}$;
(2)$( - 3.7) × ( - 3.7) × ( - 3.7) × ( - 3.7) × 5 × 5 = ( - 3.7)^{4} × 5^{2}$。
(1)$\left( + \frac{2}{5} \right) × \left( + \frac{2}{5} \right) × \left( + \frac{2}{5} \right) × \left( + \frac{2}{5} \right) = \left( + \frac{2}{5} \right)^{4} = \left( \frac{2}{5} \right)^{4}$;
(2)$( - 3.7) × ( - 3.7) × ( - 3.7) × ( - 3.7) × 5 × 5 = ( - 3.7)^{4} × 5^{2}$。
【例2】计算:(1)$(-5)^{4}$;(2)$-5^{4}$;(3)$(-\frac{2}{3})^{3}$;(4)$-\frac{2^{3}}{3}$。
[听课笔记]
_
_
_
_
名师点拨 有理数乘方运算的一般步骤
(1)定符号,幂的符号是由底数和指数决定的,通常是“先看底数,再看指数”。
(2)定绝对值,计算底数绝对值的幂。
[听课笔记]
_
_
_
_
名师点拨 有理数乘方运算的一般步骤
(1)定符号,幂的符号是由底数和指数决定的,通常是“先看底数,再看指数”。
(2)定绝对值,计算底数绝对值的幂。
答案:
1.解
(1)$( - 5)^{4} = 5^{4} = 5 × 5 × 5 × 5 = 625$;
(2)$-5^{4} = -5 × 5 × 5 × 5 = -625$;
(3)$\left( - \frac{2}{3} \right)^{3} = - \frac{2}{3} × \frac{2}{3} × \frac{2}{3} = - \frac{8}{27}$;
(4)$- \frac{2^{3}}{3} = - \frac{2 × 2 × 2}{3} = - \frac{8}{3}$。
(1)$( - 5)^{4} = 5^{4} = 5 × 5 × 5 × 5 = 625$;
(2)$-5^{4} = -5 × 5 × 5 × 5 = -625$;
(3)$\left( - \frac{2}{3} \right)^{3} = - \frac{2}{3} × \frac{2}{3} × \frac{2}{3} = - \frac{8}{27}$;
(4)$- \frac{2^{3}}{3} = - \frac{2 × 2 × 2}{3} = - \frac{8}{3}$。
【对点训练2】计算:
(1)$(-4)^{3}$;(2)$-4^{3}$;(3)$(-2)^{4}$;(4)$-2^{4}$;(5)$(\frac{3}{5})^{3}$;(6)$\frac{3^{3}}{5}$。
(1)$(-4)^{3}$;(2)$-4^{3}$;(3)$(-2)^{4}$;(4)$-2^{4}$;(5)$(\frac{3}{5})^{3}$;(6)$\frac{3^{3}}{5}$。
答案:
1.解
(1)$( - 4)^{3} = ( - 4) × ( - 4) × ( - 4) = -64$;
(2)$-4^{3} = -4 × 4 × 4 = -64$;
(3)$( - 2)^{4} = ( - 2) × ( - 2) × ( - 2) × ( - 2) = 16$;
(4)$-2^{4} = -2 × 2 × 2 × 2 = -16$;
(5)$\left( \frac{3}{5} \right)^{3} = \frac{3}{5} × \frac{3}{5} × \frac{3}{5} = \frac{27}{125}$;
(6)$\frac{3^{3}}{5} = \frac{3 × 3 × 3}{5} = \frac{27}{5}$。
(1)$( - 4)^{3} = ( - 4) × ( - 4) × ( - 4) = -64$;
(2)$-4^{3} = -4 × 4 × 4 = -64$;
(3)$( - 2)^{4} = ( - 2) × ( - 2) × ( - 2) × ( - 2) = 16$;
(4)$-2^{4} = -2 × 2 × 2 × 2 = -16$;
(5)$\left( \frac{3}{5} \right)^{3} = \frac{3}{5} × \frac{3}{5} × \frac{3}{5} = \frac{27}{125}$;
(6)$\frac{3^{3}}{5} = \frac{3 × 3 × 3}{5} = \frac{27}{5}$。
1. $(-2)^{5}$表示(
A.$2$乘$-5$
B.$2$个$-5$相加
C.$5$个$-2$相加
D.$5$个$-2$相乘
D
)A.$2$乘$-5$
B.$2$个$-5$相加
C.$5$个$-2$相加
D.$5$个$-2$相乘
答案:
1.D
2. 下列说法中不正确的是(
A.$5^{4}$表示$4$个$5$相乘
B.绝对值等于它本身的数只有$0$和$1$
C.$-6^{2}$与$(-6)^{2}$互为相反数
D.既不是正数,也不是负数的只有$0$
B
)A.$5^{4}$表示$4$个$5$相乘
B.绝对值等于它本身的数只有$0$和$1$
C.$-6^{2}$与$(-6)^{2}$互为相反数
D.既不是正数,也不是负数的只有$0$
答案:
2.B
3. 下列可以表示$7^{a}$的是(
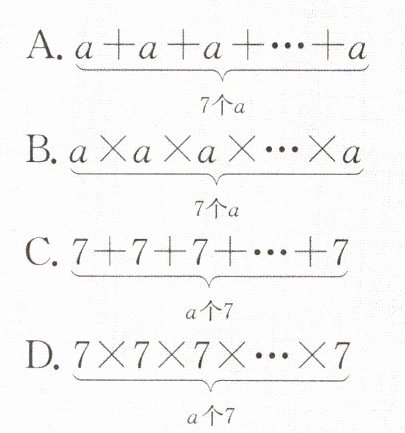
A.$\underbrace{a + a + a + \cdots + a}_{7个a}$
B.$\underbrace{a× a× a× \cdots × a}_{7个a}$
C.$\underbrace{7 + 7 + 7 + \cdots + 7}_{a个7}$
D.$\underbrace{7× 7× 7× \cdots × 7}_{a个7}$
D
)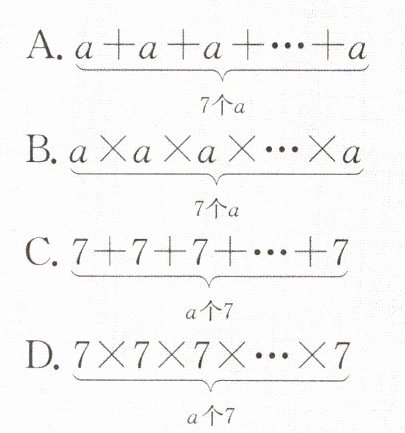
A.$\underbrace{a + a + a + \cdots + a}_{7个a}$
B.$\underbrace{a× a× a× \cdots × a}_{7个a}$
C.$\underbrace{7 + 7 + 7 + \cdots + 7}_{a个7}$
D.$\underbrace{7× 7× 7× \cdots × 7}_{a个7}$
答案:
3.D 解析$7^{a}$表示$a$个$7$相乘,即$7 × 7 × 7 × \cdots × 7$。故
选D。
选D。
4. 把一张长方形的纸对折,可得到一条折痕,继续对折,对折时每次折痕与上次的折痕保持平行,连续对折$6$次后得到(
A.$14$
B.$31$
C.$63$
D.$127$
C
)条折痕。A.$14$
B.$31$
C.$63$
D.$127$
答案:
4.C
查看更多完整答案,请扫码查看


