第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
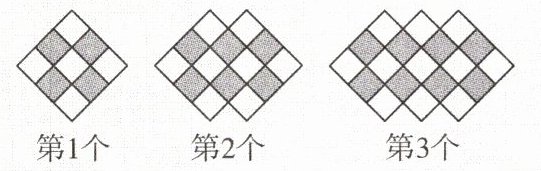
5. 如图,用灰、白两色正方形瓷砖铺设地面,第n个图案中白色瓷砖有
(3n + 2)
块。
答案:
5.(3n + 2) 解析 观察可知,第1个图案中白色瓷砖的块数为1+3+1=5,
第2个图案中白色瓷砖的块数为2+4+2=8,
第3个图案中白色瓷砖的块数为3+5+3=11,
依此规律可以得到第n个图案中白色瓷砖的块数为n+(n + 2)+n=3n + 2。
第2个图案中白色瓷砖的块数为2+4+2=8,
第3个图案中白色瓷砖的块数为3+5+3=11,
依此规律可以得到第n个图案中白色瓷砖的块数为n+(n + 2)+n=3n + 2。
6. 观察日历:
(1)用一个长方形去框图中的4个数(如图中深色方框所示),则方框内两条对角线上2个数的和有什么关系?请用代数式表示出你发现的规律,并说明其正确性。
(2)用一个长方形去框图中的9个数(如图中的斜线方框所示),你知道它们之间有什么关系吗?请用代数式表示,写出两个正确的结论,并说明它们的正确性。

(1)用一个长方形去框图中的4个数(如图中深色方框所示),则方框内两条对角线上2个数的和有什么关系?请用代数式表示出你发现的规律,并说明其正确性。
(2)用一个长方形去框图中的9个数(如图中的斜线方框所示),你知道它们之间有什么关系吗?请用代数式表示,写出两个正确的结论,并说明它们的正确性。

答案:
6.解
(1)方框内两条对角线上2个数的和相等。理由:若用a表示左上角的数,则右上角的数为a + 1,左下角的数为a + 7,右下角的数为a + 8,而a + a + 8=2a + 8,a + 1 + a + 7=2a + 8,所以结论成立。
(2)若用x表示最中间的一个数,则这9个数可分别表示为x - 8,x - 7,x - 6,x - 1,x,x + 1,x + 6,x + 7,x + 8。
①9个数的和是中间数的9倍,理由:
x - 8 + x - 7 + x - 6 + x - 1 + x + x + 1 + x + 6 + x + 7 + x + 8=9x;
②方框内对角线上3个数的和相等,理由:x - 8 + x + x + 8=3x,x - 6 + x + x + 6=3x(答案不唯一)。
(1)方框内两条对角线上2个数的和相等。理由:若用a表示左上角的数,则右上角的数为a + 1,左下角的数为a + 7,右下角的数为a + 8,而a + a + 8=2a + 8,a + 1 + a + 7=2a + 8,所以结论成立。
(2)若用x表示最中间的一个数,则这9个数可分别表示为x - 8,x - 7,x - 6,x - 1,x,x + 1,x + 6,x + 7,x + 8。
①9个数的和是中间数的9倍,理由:
x - 8 + x - 7 + x - 6 + x - 1 + x + x + 1 + x + 6 + x + 7 + x + 8=9x;
②方框内对角线上3个数的和相等,理由:x - 8 + x + x + 8=3x,x - 6 + x + x + 6=3x(答案不唯一)。
7. 如图,观察图形及图形所对应的算式,根据你发现的规律计算$1 + 8 + 16 + 24 + \cdots + 8n$(n是正整数)的结果为(

A.$(2n + 1)^2$
B.$(2n - 1)^2$
C.$(n + 2)^2$
D.$n^2$
A
)
A.$(2n + 1)^2$
B.$(2n - 1)^2$
C.$(n + 2)^2$
D.$n^2$
答案:
7.A 解析 图
(1):1+8=9=(2×1 + 1)²;
图
(2):1+8+16=25=(2×2 + 1)²;
图
(3):1+8+16+24=49=(3×2 + 1)²;
那么,图(n):1+8+16+24+…+8n=(2n + 1)²。
(1):1+8=9=(2×1 + 1)²;
图
(2):1+8+16=25=(2×2 + 1)²;
图
(3):1+8+16+24=49=(3×2 + 1)²;
那么,图(n):1+8+16+24+…+8n=(2n + 1)²。
8. 观察图中的日历图,其中用粗实线框出的六个小正方形恰好是一个正方体的展开图。
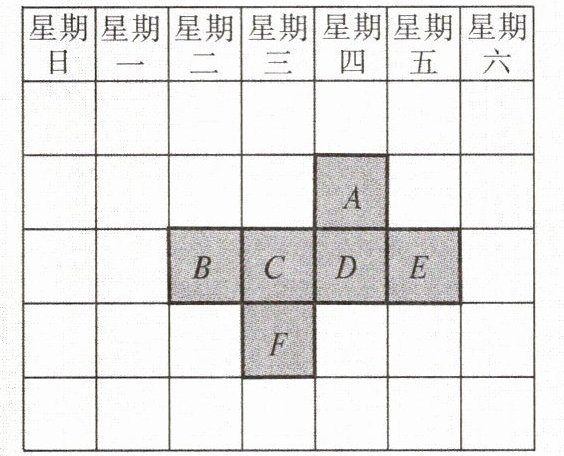
(1)如果C所在方格内的数字是16,那么A所在方格内的数字是几?
(2)若A所在方格内的数字是a,如果把此展开图折叠成原来的正方体,请用含a的代数式表示A所对的面内的数字。

(1)如果C所在方格内的数字是16,那么A所在方格内的数字是几?
(2)若A所在方格内的数字是a,如果把此展开图折叠成原来的正方体,请用含a的代数式表示A所对的面内的数字。
答案:
8.解
(1)如图,A所在的方格内的数字是10。
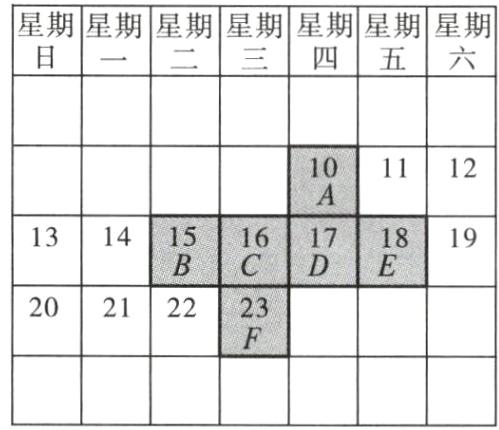
(2)把展开图复原成正方体,则A所对的面是F。如果A所在的方格内的数字是a,那么F所在的方格内的数字就是a + 13。
即A所对的面内的数字是a + 13。
8.解
(1)如图,A所在的方格内的数字是10。

(2)把展开图复原成正方体,则A所对的面是F。如果A所在的方格内的数字是a,那么F所在的方格内的数字就是a + 13。
即A所对的面内的数字是a + 13。
知识点 数字规律
用代数式表示数的变化规律:
(1)数字为整数,考虑相邻两数的和、差、积、商、符号等方面是否存在规律,也可以是奇、偶、平方等方面的规律;
(2)数字为分数,可分别观察分子、分母的变化规律及它们之间的联系。
用代数式表示数的变化规律:
(1)数字为整数,考虑相邻两数的和、差、积、商、符号等方面是否存在规律,也可以是奇、偶、平方等方面的规律;
(2)数字为分数,可分别观察分子、分母的变化规律及它们之间的联系。
答案:
答题卡作答如下:
若题目为:观察数列$ 2, 4, 6, 8, 10, \ldots $,用代数式表示其变化规律。
观察数列,发现数列中的每一项都是偶数,且每一项与前一项的差为2,即这是一个等差数列,首项为2,公差为2。
因此,可以用代数式 $2n$($n$ 为正整数)来表示这个数列的变化规律。
若题目为:观察数列 $1, \frac{3}{4}, \frac{5}{9}, \frac{7}{16}, \frac{9}{25}, \ldots$,用代数式表示其变化规律。
观察数列,分子是一个奇数数列,即 $1, 3, 5, 7, 9, \ldots$,可以表示为 $2n - 1$($n$ 为正整数);
分母是一个平方数列,即 $1^2, 2^2, 3^2, 4^2, 5^2, \ldots$,可以表示为 $n^2$。
因此,这个数列的变化规律可以用代数式 $\frac{2n - 1}{n^{2}}$($n$ 为正整数)来表示。
若题目为:观察数列$ 2, 4, 6, 8, 10, \ldots $,用代数式表示其变化规律。
观察数列,发现数列中的每一项都是偶数,且每一项与前一项的差为2,即这是一个等差数列,首项为2,公差为2。
因此,可以用代数式 $2n$($n$ 为正整数)来表示这个数列的变化规律。
若题目为:观察数列 $1, \frac{3}{4}, \frac{5}{9}, \frac{7}{16}, \frac{9}{25}, \ldots$,用代数式表示其变化规律。
观察数列,分子是一个奇数数列,即 $1, 3, 5, 7, 9, \ldots$,可以表示为 $2n - 1$($n$ 为正整数);
分母是一个平方数列,即 $1^2, 2^2, 3^2, 4^2, 5^2, \ldots$,可以表示为 $n^2$。
因此,这个数列的变化规律可以用代数式 $\frac{2n - 1}{n^{2}}$($n$ 为正整数)来表示。
查看更多完整答案,请扫码查看


