2025年金学典同步解析与测评贵州人民出版社八年级数学上册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金学典同步解析与测评贵州人民出版社八年级数学上册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
2. 下列说法正确的是(
A.所有的命题都有逆命题
B.假命题的逆命题一定是假命题
C.假命题没有逆命题
D.真命题的逆命题一定是真命题
A
).A.所有的命题都有逆命题
B.假命题的逆命题一定是假命题
C.假命题没有逆命题
D.真命题的逆命题一定是真命题
答案:
A
3. 如图,直线CD是线段AB的垂直平分线,P为直线CD上一点. 若△PAB的周长为16,PA= 5,则线段AB的长为(
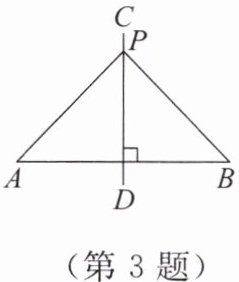
A.10
B.6
C.5
D.3
B
).
A.10
B.6
C.5
D.3
答案:
B
4. 如图,DE是AC的垂直平分线,AD= 4,△ABE的周长为11,则△ABC的周长为(
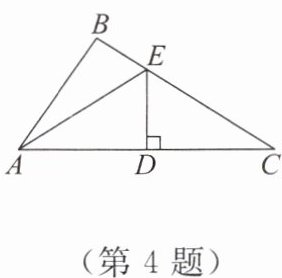
A.30
B.26
C.19
D.14
C
).
A.30
B.26
C.19
D.14
答案:
C
5. 如图,在△ABC中,边AB的垂直平分线$l_1$交BC于点D,边AC的垂直平分线$l_2$交BC于点$E,l_1$与$l_2$相交于点O,连接OA,OB,OC. 若△ADE的周长为9 cm,△OBC的周长为21 cm,求BC,OA的长.


答案:
【解】因为l₁垂直平分AB,
所以DA=DB,OB=OA.
同理,EA=EC,OC=OA.
所以DA+DE+EA=BD+DE+EC=BC.
因为△ADE的周长为9 cm,
所以BC=9 cm.
因为△OBC的周长为21 cm,
所以OB+OC+BC=21 cm.
所以OB+OC=21 - 9 = 12(cm).
所以OA=OB=OC=6 cm.
所以DA=DB,OB=OA.
同理,EA=EC,OC=OA.
所以DA+DE+EA=BD+DE+EC=BC.
因为△ADE的周长为9 cm,
所以BC=9 cm.
因为△OBC的周长为21 cm,
所以OB+OC+BC=21 cm.
所以OB+OC=21 - 9 = 12(cm).
所以OA=OB=OC=6 cm.
6. (1)【发现问题】如图(1),在△ABE与△ACF中,AB= AE,AC= AF,∠BAE= ∠CAF,B,F,C三点在同一条直线上,连接EF交AB于点D,求线段BC与ED,DF的数量关系,并说明理由.
(2)【类比探究】如图(2),在Rt△ABC中,∠ABC= 90°,以AC为边,作△ACD,满足AD= AC,E为BC上一点,连接AE,2∠BAE= ∠CAD,连接DE,求证DE= CE+2BE.

(2)【类比探究】如图(2),在Rt△ABC中,∠ABC= 90°,以AC为边,作△ACD,满足AD= AC,E为BC上一点,连接AE,2∠BAE= ∠CAD,连接DE,求证DE= CE+2BE.

答案:
【解】(1)BC=ED+DF. 理由如下.
因为∠BAE=∠CAF,
所以∠BAE+∠BAF=∠CAF+∠BAF,即∠EAF=∠BAC.
在△BAC和△EAF中,
{AB=AE,
∠BAC=∠EAF,
AC=AF,
所以△BAC≌△EAF(SAS).
所以BC=EF.
又因为EF=ED+DF,
所以BC=ED+DF.
【证明】(2)延长EB至点G,使BG=BE,连接AG(图略).
因为∠ABC=90°,所以AB⊥GE.
所以AB垂直平分GE. 所以AG=AE.
又因为AB=AB,
所以Rt△ABG≌Rt△ABE(HL).
所以∠BAG=∠BAE.
所以∠GAE=2∠BAE=∠CAD.
所以∠GAE+∠EAC=∠CAD+∠EAC,即∠GAC=∠EAD.
在△GAC与△EAD中,
{AG=AE,
∠GAC=∠EAD,
AC=AD,
所以△GAC≌△EAD(SAS).
所以DE=GC=EC+GE=CE+2BE,
即DE=CE+2BE.
因为∠BAE=∠CAF,
所以∠BAE+∠BAF=∠CAF+∠BAF,即∠EAF=∠BAC.
在△BAC和△EAF中,
{AB=AE,
∠BAC=∠EAF,
AC=AF,
所以△BAC≌△EAF(SAS).
所以BC=EF.
又因为EF=ED+DF,
所以BC=ED+DF.
【证明】(2)延长EB至点G,使BG=BE,连接AG(图略).
因为∠ABC=90°,所以AB⊥GE.
所以AB垂直平分GE. 所以AG=AE.
又因为AB=AB,
所以Rt△ABG≌Rt△ABE(HL).
所以∠BAG=∠BAE.
所以∠GAE=2∠BAE=∠CAD.
所以∠GAE+∠EAC=∠CAD+∠EAC,即∠GAC=∠EAD.
在△GAC与△EAD中,
{AG=AE,
∠GAC=∠EAD,
AC=AD,
所以△GAC≌△EAD(SAS).
所以DE=GC=EC+GE=CE+2BE,
即DE=CE+2BE.
查看更多完整答案,请扫码查看


