《2025年状元成才路创优作业八年级数学上册北师大版》

1. 在$-2,π,0,\sqrt{4},\frac{1}{3},\sqrt{8}$中,无理数的个数是(C)
A.4
B.3
C.2
D.5

答案： C

2. 把下列各数填入相应的集合内：
$0,-\frac{5}{4},\sqrt{16},3.1415926,-\sqrt[3]{7},\frac{π}{3},6\%,\sqrt{2},0.5050050005…$(相邻两个5之间0的个数逐次加1),$0.1\dot{5},\sqrt[3]{-125}$。
有理数集合：…{$$}。
无理数集合：…{$$}。
整数集合：…{$$}。
分数集合：…{$$}。

答案： 有理数集合：{ 0，-5/4，√16，3.1415926，6%，0.1∙5，³√-125 }；
无理数集合：{ -³√7，π/3，√2，0.5050050005… }；
整数集合：{ 0，√16，³√-125 }；
分数集合：{ -5/4，3.1415926，6%，0.1∙5}；

3. $\sqrt{\frac{1}{16}}$的平方根是(C)
A.$\frac{1}{2}$
B.$\frac{1}{4}$
C.$\pm\frac{1}{2}$
D.$\pm\frac{1}{4}$

答案： C

4. 下列说法或等式中,正确的个数是(A)
①$\sqrt{0.9}= 0.3$；②$\sqrt{1\frac{7}{9}}= \pm\frac{4}{3}$；③$-3^{2}的平方根是-3$；④$\sqrt{(-5)^{2}}的算术平方根是-5$；⑤$\pm\frac{7}{6}是1\frac{13}{36}$的平方根。
A.1
B.2
C.3
D.4

答案： A

5. 已知$a＞b$,化简二次根式$\sqrt{-ab^{3}}$的结果正确的是(D)
A.$b\sqrt{ab}$
B.$\sqrt{-ab}$
C.$-b\sqrt{ab}$
D.$-b\sqrt{-ab}$

答案： D

6. 已知$y= \sqrt{x - 5}+\sqrt{5 - x}+8$,则$xy$的值为40。

答案： 40

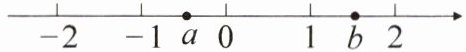
7. 实数$a,b$在数轴上的对应点的位置如图所示,则$\sqrt{(a + 1)^{2}}-\sqrt{(b - 1)^{2}}$的值为a-b+2。

答案： a-b+2

8. 新考向 过程性学习·步骤找错 课堂上,李老师出了这样一个题目：当$a = 100$时,求代数式$a+\sqrt{1 - 2a + a^{2}}$的值。小亮和小芳的解答过程如下：
小亮：原式$=a+\sqrt{(1 - a)^{2}}= a + 1 - a = 1$。
小芳：原式$=a+\sqrt{(1 - a)^{2}}= a + a - 1 = 2a - 1 = 2×100 - 1 = 199$。
(1)小亮的解法是错误的,错误的原因是______化简√(1-a)²时未考虑1-a的正负；
(2)请根据以上信息,解答下列问题：当$a = - 100$时,求代数式$a - 2\sqrt{a^{2} - 6a + 9}+6$的值。

答案： 解:
(1)小亮 化简√(1-a)²时未考虑1-a的正负
(2)a-2√(a²-6a+9)+6=-300。