第47页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A的坐标是(1,2),则经过第101次变换后点A的对应点的坐标为(

A.(1,-2)
B.(-1,-2)
C.(-1,2)
D.(1,2)
C
)
A.(1,-2)
B.(-1,-2)
C.(-1,2)
D.(1,2)
答案:
C
2. [2025·汝州期中]如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2025次运动后动点P的坐标是(
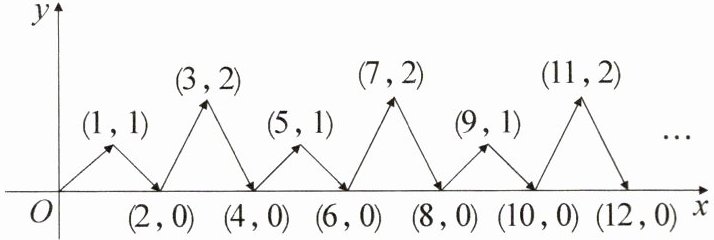
A.(2024,1)
B.(2024,0)
C.(2025,1)
D.(2025,2)
C
)
A.(2024,1)
B.(2024,0)
C.(2025,1)
D.(2025,2)
答案:
C
3. [2025·郑州期中]如图,在平面直角坐标系中,动点P按箭头所示的方向做折线运动,第1次从原点运动到点(1,0),第2次从点(1,0)运动到点(1,1),第3次从点(1,1)运动到点(2,1),第4次从点(2,1)运动到点(2,-1),第5次从点(2,-1)运动到点(3,-1),第6次从点(3,-1)运动到点(3,2)……按这样的运动规律(向右始终保持运动一个单位长度,向上或向下比前一次的向下或向上都多运动一个单位长度),第2024次运动后,点P的坐标是(
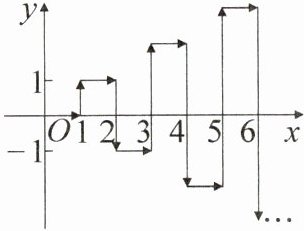
A.(1011,506)
B.(1011,-506)
C.(1012,506)
D.(1012,-506)
D
)
A.(1011,506)
B.(1011,-506)
C.(1012,506)
D.(1012,-506)
答案:
D
4. 如图,在平面直角坐标系中,一动点自点P₀(1,0)处向上运动1个单位长度至点$P_1(1,1)$处,然后向左运动2个单位长度至点$P_2(-1,1)$处,再向下运动3个单位长度至点$P_3(-1,-2)$处,再向右运动4个单位长度至点$P_4(3,-2)$处……按如此规律继续运动下去,当这点运动至点$P_2₀_2_4$处时,点$P_2₀_2_4$的坐标是(
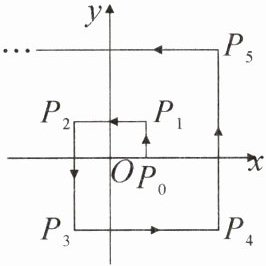
A.(-1011,1011)
B.(1011,-1012)
C.(1013,-1012)
D.(1013,1013)
C
)
A.(-1011,1011)
B.(1011,-1012)
C.(1013,-1012)
D.(1013,1013)
答案:
C
5. 如图,在平面直角坐标系中,已知点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一条长为2024个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是(
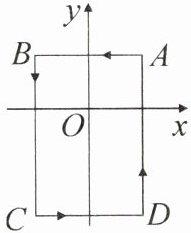
A.(-1,0)
B.(1,-2)
C.(1,-1)
D.(-1,-1)
D
)
A.(-1,0)
B.(1,-2)
C.(1,-1)
D.(-1,-1)
答案:
D
查看更多完整答案,请扫码查看


