《2025年状元成才路创优作业八年级数学上册北师大版》

7. [2025·平顶山宝丰县期末]《孙子算经》中有这样一个问题：“今有三人共车,二车空；二人共车,九人步。问：人与车各几何？”题目大意：若 3 人坐一辆车,则两辆车是空的；若 2 人坐一辆车,则 9 人需要步行。人与车各多少？设有 $ x $ 辆车,人数为 $ y $,根据题意,可列二元一次方程组为 (A)
A.$\begin{cases}3(x - 2) = y, \\ 2x + 9 = y\end{cases} $
B.$\begin{cases}3x - 2 = y, \\ 2x + 9 = y\end{cases} $
C.$\begin{cases}3x + 2 = y, \\ 2x + 9 = y\end{cases} $
D.$\begin{cases}3x + 2 = y, \\ 2x - 9 = y\end{cases} $

答案： A

8. 【新教材新题型：P120 例 1 变式题】我国古典数学文献《增删算法统宗·六均输》中有一个“隔沟计算”的问题：“甲乙隔沟牧放,二人暗里参详。甲云得乙九只羊,多乙一倍之上。乙说得甲九只,两家之数相当。二人闲坐恼心肠,画地算了半晌。”题目大意：甲、乙两人一起放牧,两人心里暗中数羊。如果乙给甲 9 只羊,那么甲的羊数为乙的 2 倍；如果甲给乙 9 只羊,那么两人的羊数相同,则甲有63只羊,乙有45只羊。

答案： 63 45

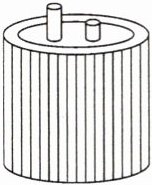
9. 如图,两根铁棒直立于桶底水平的木桶中,在木桶中加入水后,一根高出水面的长度是它的 $\frac{1}{4}$,另一根高出水面的长度是它的 $\frac{1}{7}$。若两根铁棒长度之和为 150 cm,则此时木桶中水的深度是60 cm。

答案： 60 cm

10. 《九章算术》中有这样一个题：今有二马一牛价过一万,如半马之价；一马二牛价不满一万,如半牛之价。问：牛、马价各几何？题目大意：今有 2 匹马,1 头牛的总价超过 1 万钱,其超出的钱数相当于 $\frac{1}{2}$ 匹马的价格；1 匹马,2 头牛的总价不足 1 万钱,所差的钱数相当于 $\frac{1}{2}$ 头牛的价格。每头牛、每匹马的价格各是多少？

答案： 解:每头牛的价格为$\frac {2}{11}$万钱,每匹马的价格为$\frac {6}{11}$万钱。

11. 某包装厂承接了一批纸盒加工任务,计划用如图①所示的长方形和正方形纸板做侧面和底面,做成如图②所示的竖式与横式两种无盖的长方体纸盒(拼接即可,不需裁剪)。

(1) 做 1 个竖式纸盒和 2 个横式纸盒,需要正方形纸板5块,需要长方形纸板10块；
(2) 现在仓库里有 2000 块正方形纸板和 4000 块长方形纸板,两种纸盒各做多少个,恰好使库存的纸板用完？
竖式纸盒做400个,横式纸盒做800个。

答案： （1）5 10 （2）竖式纸盒做400个,横式纸盒做800个。