《2025年状元成才路创优作业八年级数学上册北师大版》

11. 一个数的算术平方根是它本身,则这个数是 (C)
A.0
B.1
C.0,1
D.0,±1

答案： C

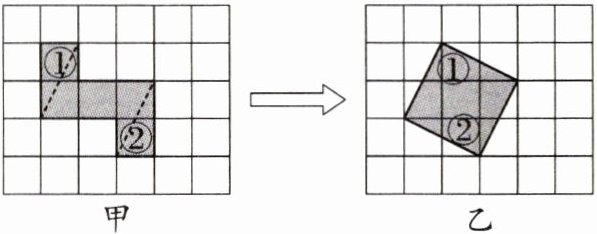
12. 新考向 动手操作 已知每个小正方形的边长均为 1,将图甲中阴影部分沿虚线分割后,可重新拼成如图乙所示的正方形,那么所拼成的正方形的边长为 (C)

A.$\sqrt{3}$
B.2
C.$\sqrt{5}$
D.$\sqrt{6}$

答案： C

13. 新考向 跨物理·电流热效应 电流通过导线时会产生热量,电流$I$(单位：A)、导线电阻$R$(单位：Ω)、通电时间$t$(单位：s)与产生的热量$Q$(单位：J)满足$Q = I^{2}Rt$。已知导线电阻为 5 Ω,1 s 时间导线产生 30 J 的热量,则电流$I$的值为 (B)
A.$\sqrt{5}$ A
B.$\sqrt{6}$ A
C.$\sqrt{10}$ A
D.$\sqrt{30}$ A

答案： B

14. [2025·郑州中牟县期末]一个数值转换器的原理如图所示,当输入的$x = 256$时,输出的$y$等于 $\sqrt{2}$。

答案： $\sqrt{2}$

15. 已知$x= \sqrt{25}$,$\sqrt{y}= 2$,$z$是 9 的算术平方根,求$2x + y - z$的算术平方根。

答案： 解:$2x+y-z$的算术平方根是$\sqrt{11}$。

16. 新考向 规律探索 找出规律并解答问题。
(1)填写下表：

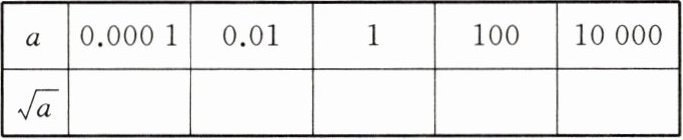
上表中数$a的小数点的移动与它的算术平方根\sqrt{a}$的小数点的移动有何规律？
规律:数a的小数点每向左(或右)移动两位,$\sqrt{a}$的小数点就相应地向左(或右)移动一位。
(2)已知$\sqrt{15}= k$,$\sqrt{0.15}= a$,$\sqrt{1500}= b$,直接用含$k的式子分别表示a$,$b$。
$a=0.1k$,$b=10k$。

答案： 解:
(1)0.01 0.1 1 10 100
规律:数a的小数点每向左(或右)移动两位,$\sqrt{a}$的小数点就相应地向左(或右)移动一位。
(2)$a=0.1k$,$b=10k$。

1. 若$\vert a - 2\vert + \sqrt{a + b} = 0$,则 $ab$ 的值为-4。

答案： -4

2. 若$\sqrt{x - 1} + (y + 2)^2 = 0$,则$(x + y)^{2025} = $-1。

答案： -1

3. 若$\sqrt{x - 6} + \sqrt{y + 4} = 0$,则 $x - 2y$ 的算术平方根是$\sqrt{14}$。

答案： $\sqrt{14}$

4. 若$(a + 1)^2 + \vert b - 2\vert + \sqrt{c + 3} = 0$,求 $a(b + c)$ 的值。

答案： 解:$a(b+c)=1$。