《2025年状元成才路创优作业八年级数学上册北师大版》

1. 下列函数中,是正比例函数的是(C)
A.$ y = x ^ { 2 } $
B.$ y = - \frac { 1 } { 2 } x + 1 $
C.$ y = - \frac { 1 } { 2 } x $
D.$ y = a x $

答案： C

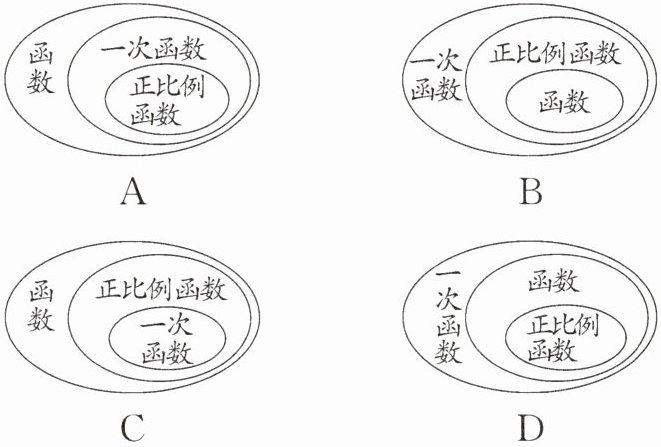
2. 函数、一次函数和正比例函数之间的包含关系是(A)
]

答案： A

3. 若 $ y = ( m - 2 ) x + 1 $ 是关于 $ x $ 的一次函数,则 $ m $ 的取值范围是m≠2。

答案： m≠2

变式题 [条件变式]若 $ y = 2 x - m + 3 $ 是关于 $ x $ 的正比例函数,则 $ m $ 的值是3。

答案： 3

4. 某种商品的售价为每件 150 元,若按现售价的八折进行促销,设购买 $ x $ 件需要 $ y $ 元,则 $ y $ 与 $ x $ 之间的关系式为(C)
A.$ y = 0.8 x $
B.$ y = 30 x $
C.$ y = 120 x $
D.$ y = 150 x $

答案： C

5. 新考向 情境题·烤鸭 某烤鸭店在确定烤鸭的烤制时间时,主要依据的是表中的数据：

设鸭的质量为 $ x $ kg,烤制时间为 $ t $ min。则 $ t $ 与 $ x $ 之间的关系式是t=40x+20。

答案： t=40x+20

6. 写出下列各题中 $ y $ 与 $ x $ 之间的关系式,并判断：$ y $ 是否为 $ x $ 的一次函数？是否为正比例函数？
(1) 正方形的面积 $ y $(单位：$ \mathrm { cm } ^ { 2 } $)与它的边长 $ x $(单位：$ \mathrm { cm } $)之间的关系；
(2) 某地居民用电收费标准是 $ 0.53 $ 元/($ \mathrm { kW } \cdot \mathrm { h } $),应缴电费 $ y $(单位：元)与用电量 $ x $(单位：$ \mathrm { kW } \cdot \mathrm { h } $)之间的关系；
(3) 汽车从离 $ A $ 站 $ 4 $ km 的 $ B $ 地出发,以 $ 40 $ km/h 的速度沿射线 $ A B $ 方向匀速行驶,汽车到 $ A $ 站的距离 $ y $(单位：km)与匀速行驶的时间 $ x $(单位：h)之间的关系。

答案： 解:
(1)y=x²,y 不是 x 的一次函数,也不是 x 的正比例函数。
(2)y=0.53x,y 是 x 的一次函数,也是 x 的正比例函数。
(3)y=40x+4,y 是 x 的一次函数,但不是 x 的正比例函数。

7. 【教材 P82 例 2 变式题】某水库的水位以 $ 0.2 $ m/h 的速度匀速上涨。
(1) 假设该水库的初始水位高度为 $ 20 $ m,试写出水库的水位高度 $ y $(单位：m)与水位上涨的时间 $ x $(单位：h)之间的关系式 $ y = k x + b $,并说明 $ k $ 和 $ b $ 的实际意义；
(2) 求出当水库的水位高度为 $ 24 $ m 时,水位上涨的时间。

答案： 解:
(1)y=0.2x+20,k=0.2 表示每小时水位高度的变化量,b=20 表示水位上涨开始时的高度。
(2)水位上涨的时间为 20 h。