《2025年状元成才路创优作业八年级数学上册北师大版》

一筐苹果,三三数之余二,四四数之余一,五五数之不足一,这筐苹果最少有多少个？
解：(1)这筐苹果的数量应同时满足：苹果的数量为正整数,且满足以下三个条件：
①除以 3 余 2；②除以 4 余 1；③除以 5 不足 1,即余 4。
(2)逐步确定满足以上三个条件的最小正整数。
符合条件①的正整数有：2,5,8,11,14,17,20,23,26,29,32,35,38,41,…$$。(A)
在(A)中,符合条件②的正整数有：5,17,29,41,…$$。(B)
在(B)中,符合条件③的正整数有：29,…$$。
因此,同时满足三个条件的最小正整数是29。所以,这筐苹果最少有29个。

答案： 5,17,29,41 29 29 29

1. 有一串珠子,5 颗 5 颗地数,正好数尽,7 颗 7 颗地数,最后余 4 颗,这串珠子至少有25颗。

答案： 25

2. 若三位数$\overline{5ab}$能被 6 整除,这个数最大是多少？

答案： 解：这个数最大是594。

3. 如图,在平面直角坐标系中,已知点$A( - 3,0)$,$B(1,0)$,$C(0,3)$,$D(0, - 4)$。在平面内有一点$E$,使得$S_{\triangle ABE}= S_{\triangle ABC}$,$S_{\triangle DOE}= S_{\triangle ACD}$,求点$E$的坐标。

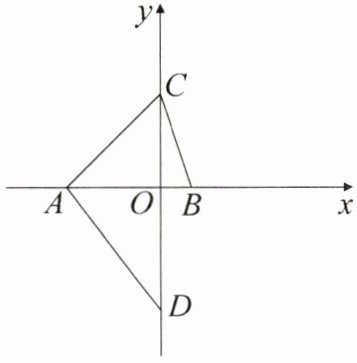
答案： 解：点E的坐标为$\left( \frac{21}{4},3 \right)$或$\left( -\frac{21}{4},3 \right)$或$\left( \frac{21}{4},-3 \right)$或$\left( -\frac{21}{4},-3 \right)$。