《2025年状元成才路创优作业八年级数学上册北师大版》

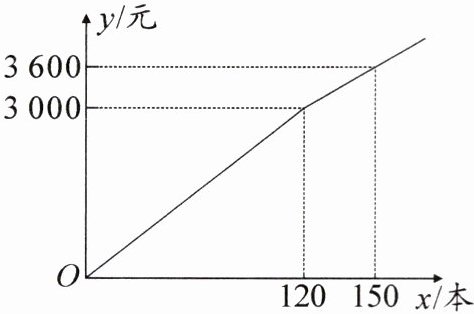
1. 每年4月23日是世界读书日,旨在推动更多的人去阅读和写作。某书店以读书日为契机,决定购进甲、乙两种图书,供消费者选择。经调查,乙种图书每本进价20元,甲种图书的总进价y(单位：元)与购进甲种图书的数量x(单位：本)之间的关系如图所示。
(1) 请求出当$0\leqslant x\leqslant 120和x＞120$时,y与x之间的关系式。
(2) 若该书店准备购进甲、乙两种图书共300本,且每种图书的数量都不少于120本,书店计划甲种图书以每本30元的价格出售,乙种图书以每本25元的价格出售,如何购进两种图书,才能使书店所获利润最大？最大利润是多少？

答案： 1.解:
(1)当0≤x≤120时,y=25x;当x＞120时,y=20x+600。
(2)购进甲种图书180本,乙种图书120本,才能使书店所获利润最大,最大利润是1800元。

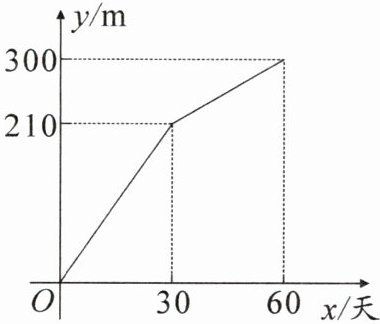
2. 甲、乙两个工程组同时挖掘某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和y(单位：m)与甲组挖掘时间x(单位：天)之间的关系如图所示。
(1) 甲组比乙组多挖掘了30天；
(2) 求乙组停工后y与x之间的关系式,并写出自变量x的取值范围；
(3) 当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组已停工的天数。

(2)y=3x+120(30≤x≤60)。
(3)乙组已停工10天。

答案： 2.解:
(1)30
(2)y=3x+120(30≤x≤60)。
(3)乙组已停工10天。

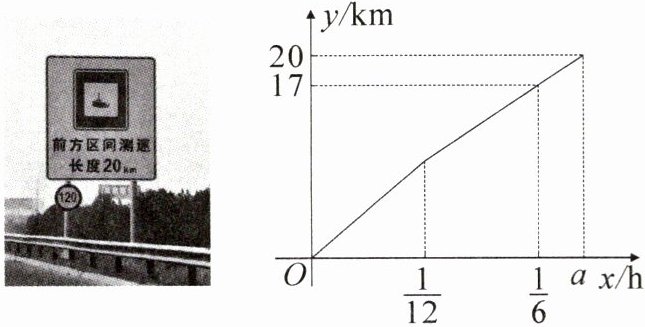
3. 新考向 情境题·区间测速 [2024·长春中考]小春驾驶一辆小型汽车在高速公路上行驶,其间经过一段长度为20 km的区间测速路段,从该路段起点开始,他先匀速行驶$\frac{1}{12}$h,再立即减速以另一速度匀速行驶(减速时间忽略不计),当他到达该路段终点时,测速装置测得该辆汽车在整个路段行驶的平均速度为100 km/h。汽车在区间测速路段行驶的路程y(单位：km)与在此路段行驶的时间x(单位：h)之间的关系如图所示。
(1) a的值为$\frac{1}{5}$；
(2) 当$\frac{1}{12}\leqslant x\leqslant a$时,求y与x之间的关系式；
(3) 通过计算说明在此区间测速路段内,该辆汽车减速前是否超速(此路段要求小型汽车行驶速度不得超过120 km/h)。

答案： 3.解:
(1)$\frac{1}{5}$
(2)y=90x+2($\frac{1}{12}$≤x≤$\frac{1}{5}$)。
(3)当x=$\frac{1}{12}$时,y=90×$\frac{1}{12}$+2=9.5,
所以先匀速行驶$\frac{1}{12}$h的速度为9.5÷$\frac{1}{12}$=114(km/h)。
因为114＜120,所以这辆汽车减速前没有超速。