第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
【例 4】水库中水位第一天连续上升了 $b$ h,平均每小时上升 $2$ cm,第二天连续下降了 $b$ h,平均每小时下降 $0.25$ cm,第三天连续下降了 $b$ h,平均每小时下降 $2.5$ cm,这三天水位的总变化量是多少?
解:
【规律方法】
(1)多项式的化简求值,一般是先化简,再求值,即先合并同类项,直到式子中没有同类项后,再将字母的值代入计算结果. 代入时,若所给的字母的值是负数,需加括号,计算过程中要注意运算顺序.
(2)利用合并同类项解决实际问题时,要先找出题目中的数量关系,并根据数量关系列式,再合并同类项,最后得出结论.
解:
【规律方法】
(1)多项式的化简求值,一般是先化简,再求值,即先合并同类项,直到式子中没有同类项后,再将字母的值代入计算结果. 代入时,若所给的字母的值是负数,需加括号,计算过程中要注意运算顺序.
(2)利用合并同类项解决实际问题时,要先找出题目中的数量关系,并根据数量关系列式,再合并同类项,最后得出结论.
答案:
解:这三天水位的总变化量是下降了0.75b cm(或上升了-0.75b cm).
4. 先化简,再求值:$-x^{2} + 5x + 4 + 5x - 4 + 2x^{2}$,其中 $x = -2$.
答案:
解:原式=$x^{2}+10x$.当$x=-2$时,原式=-16.
5. 某食堂原有 $30$ 袋面粉,每袋面粉的质量为 $m$ kg. 该食堂昨天中午用去 $15$ 袋面粉,下午又购进同样包装的面粉 $100$ 袋,晚上又用去 $16$ 袋,则该食堂现有面粉多少千克?
答案:
解:该食堂现有面粉99m kg.
纸盒的制作与摆放
某班综合实践小组开展“制作纸盒”的实践活动.
【知识准备】
下列各组单项式中,是同类项的是
① $2$ 和 $b$; ② $-2$ 和 $5$; ③ $-3x^{2}y$ 和 $2x^{2}y$; ④ $2a$ 和 $3b$.
【制作纸盒】
综合实践小组准备制作正方体、长方体两种纸盒,已知尺寸如下表所示.

要制作这两种纸盒各 $1$ 个,一共用纸的面积是
【拓展探究】
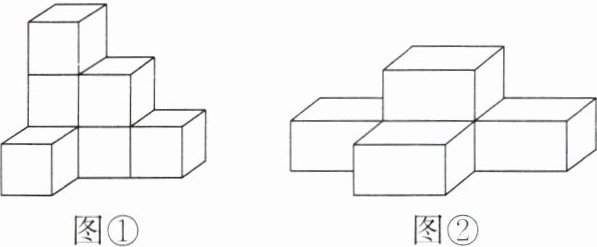
综合实践小组一共制作了 $7$ 个相同的正方体纸盒和 $5$ 个相同的长方体纸盒,他们继续探究,把 $7$ 个正方体纸盒摆放成了如图①所示的形状,把 $5$ 个长方体纸盒摆放成了如图②所示的形状,则图①中的图形的表面积是
某班综合实践小组开展“制作纸盒”的实践活动.
【知识准备】
下列各组单项式中,是同类项的是
②③
.(只填序号)① $2$ 和 $b$; ② $-2$ 和 $5$; ③ $-3x^{2}y$ 和 $2x^{2}y$; ④ $2a$ 和 $3b$.
【制作纸盒】
综合实践小组准备制作正方体、长方体两种纸盒,已知尺寸如下表所示.

要制作这两种纸盒各 $1$ 个,一共用纸的面积是
$6c^{2}+2ab+2bc+2ac$
$cm^{2}$.(黏合处及损耗忽略不计)【拓展探究】
综合实践小组一共制作了 $7$ 个相同的正方体纸盒和 $5$ 个相同的长方体纸盒,他们继续探究,把 $7$ 个正方体纸盒摆放成了如图①所示的形状,把 $5$ 个长方体纸盒摆放成了如图②所示的形状,则图①中的图形的表面积是
$28c^{2}$
$cm^{2}$;图②中的图形的表面积是$8ab+8ac+6bc$
$cm^{2}$.
答案:
【知识准备】②③ 【制作纸盒】($6c^{2}+2ab+2bc+2ac$) 【拓展探究】$28c^{2}$ ($8ab+8ac+6bc$)
查看更多完整答案,请扫码查看


