《2025年人教金学典同步解析与测评七年级数学上册人教版云南专版》

7. 一组有规律的图案如图所示,它由若干个大小相同的圆片组成。第$1个图案中有4$个白色圆片,第$2个图案中有6$个白色圆片,第$3个图案中有8$个白色圆片,第$4个图案中有10$个白色圆片……依此规律,第$n$个图案中有(2+2n)个白色圆片(用含$n$的代数式表示)。

答案： (2+2n)

1. 下列各式中,是代数式的是(C)
A.$ S = \pi r^{2} $
B.$ 2a ＞ b $
C.$ 3x + y $
D.$ \pi \approx 3.14 $

答案： C

2. 下列代数式书写规范的是(D)
A.$ 1 \frac{2}{9} a $
B.$ 2m + n \ m $
C.$ a × 5 $
D.$ 2x^{2}y $

答案： D

3. 代数式$ -7x $的意义可以是(C)
A.$ -7 与 x $的和
B.$ -7 与 x $的差
C.$ -7 与 x $的积
D.$ -7 与 x $的商

答案： C

4. “$ 1,2,3,4,5,6,… $”表示从$ 1 $开始的连续整数,第$ n $个数用 n 表示；“$ 2,4,6,8,10,… $”为从$ 2 $开始的连续偶数,第$ m $个数可表示为2m；“$ 1,3,5,7,9,… $”为从$ 1 $开始的连续奇数,第$ p $个数可表示为2p-1。

答案： 2m 2p-1

5. 如图,请你求出阴影部分的面积(用含有$ x $的代数式表示)。

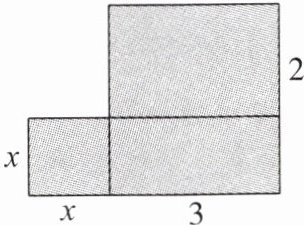
答案： 解:x²+3x+6.

6. 用代数式表示：
(1)$ x 与 y $的平方差。
(2)$ m 的 3 倍与 n $的差的平方。
(3)$ x 的 3 倍与 y 的 4 $倍的商。
(4)某班共有$ x $名学生,其中女生人数占$ 45\% $,则男生人数是多少？
(5)某种品牌的电视机降价$ 30\% $以后,每台售价为$ a $元,则该品牌电视机每台原价为多少元？

答案： 解:
(1)x²-y².
(2)(3m-n)².
(3)$\frac{3x}{4y}$.
(4)55%x.
(5)$\frac{10a}{7}$元.