《2025年学习质量监测八年级数学上册人教版》

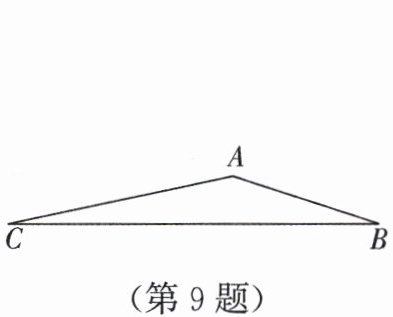
9. 某市在“旧城改造”中计划在市内一块如图所示的三角形空地上,种植某种草皮以美化环境.已知 $ AC = 30 m $,$ AB = 20 m $,$ \angle BAC = 150^{\circ} $,这种草皮每平方米的售价是 $ a $ 元,则购买这种草皮至少需要花费150a元.
]

答案： 150a

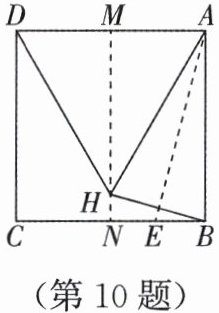
10. 如图,先将正方形纸片对折,折痕为 $ MN $,再把点 $ B $ 折叠在折痕 $ MN $ 上,折痕为 $ AE $,点 $ B $ 在 $ MN $ 上的对应点为 $ H $,沿 $ AH $ 和 $ DH $ 剪下得到 $ \triangle ADH $,有下列选项：
①$ AE $ 垂直平分 $ HB $；②$ \angle HBN = 15^{\circ} $；③$ DH = DC $；④$ \triangle ADH $ 是一个等边三角形.
其中正确的是①②③④.(请将正确选项的序号都填上)

答案： ①②③④

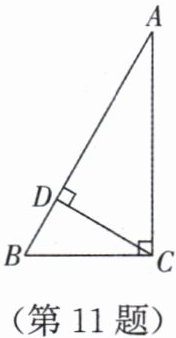
11. 如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ CD $ 是 $ AB $ 边上的高,$ \angle A = 30^{\circ} $.
(1)求 $ \angle BCD $ 的度数；
(2)若 $ BD = a $,求 $ AB $ 的长度.(用含 $ a $ 的式子表示)
]

答案： 解:
(1)
∵CD是AB边上的高,∠A=30°,
∴∠ACD=90°-∠A=90°-30°=60°.又∠ACB=90°,
∴∠BCD=90°-∠ACD=90°-60°=30°.
(2)在Rt△BCD中,∠BCD=30°,∠CDB=90°,BD=a,
∴BC=2BD=2a.在Rt△ACB中,∠A=30°,∠ACB=90°,
∴AB=2BC=4a.

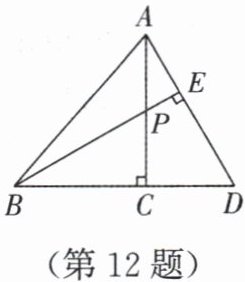
12. 如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ P $ 是 $ AC $ 的中点,过点 $ A $ 作 $ AD \perp BP $,交 $ BP $ 的延长线于点 $ E $,交 $ BC $ 的延长线于点 $ D $. 若 $ \angle DBE = 30^{\circ} $,$ BE = 10 $,求 $ PE $,$ PB $ 的长.
]

答案： 解:如图,设PE=a.
∵AD⊥BP,
∴∠DBE+∠D=90°.
∵∠ACB=90°,
∴∠DAC+∠D=90°,
∴∠DAC=∠DBE=30°,
∴AP=2a.
∵P是AC的中点,
∴CP=AP=2a.在Rt△PBC中,∠CBP=30°,∠BCP=90°,
∴BP=2CP=4a,
∴BE=BP+PE=4a+a=5a.
∵BE=10,
∴5a=10,a=2,
∴PE=2,PB=8.