《2025年学习质量监测八年级数学上册人教版》

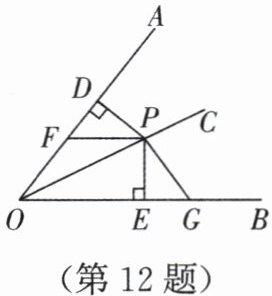
12. 如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F,G分别是OA,OB上的点,且PF= PG,DF= EG。求证：OC是∠AOB的平分线。

答案： 证明:
∵PD⊥OA,PE⊥OB,
∴∠PDF=∠PEG=90°,
在Rt△PFD和Rt△PGE中,
PF=PG,
DF=EG,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE,
∵P是OC上一点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线.

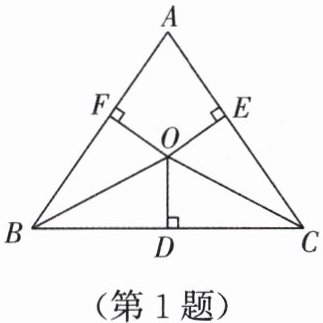
1. 如图,O是△ABC内一点,且O到三边AB,BC,CA的距离OF= OD= OE,若∠BAC= 70°,则∠BOC的度数为(C)

A.70°
B.120°
C.125°
D.130°

答案： C

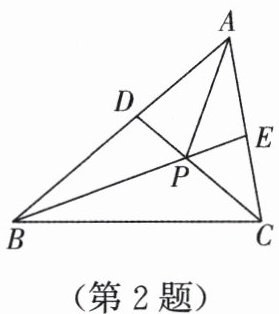
2. 如图,任意画一个∠BAC= 60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论：①∠BPC= 120°；②AP平分∠BAC；③AP= PC；④BD+CE= BC；$⑤S_{△PBD}+S_{△PCE}= S_{△PBC}。$其中,结论正确的是(A)。

A.①②④⑤
B.②③⑤
C.①②⑤
D.①②③④

答案： A

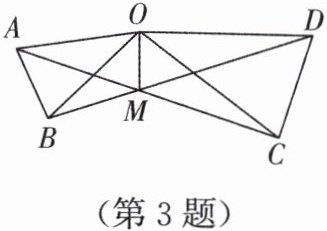
3. 如图,在△AOB和△COD中,OA= OB,OC= OD,OA ＜ OC,∠AOB= ∠COD= 36°,连接AC,BD交于点M,连接OM。有下列结论：
①AC= BD；②∠AMB= 36°；③OM平分∠AOD；④MO平分∠AMD。
其中正确结论的序号是______。(请将正确结论的序号都填上)

答案：
①②④ [提示]由题意，可得△AOC≌△BOD(SAS),
于是AC=BD,故①正确;
由全等三角形的性质，得∠OAC=∠OBD,结合三角形的外角性质,可得∠AMB+∠OBD=∠OAC+∠AOB,即∠AMB=∠AOB=36°,故②正确;如图,作OG⊥AM于点G,OH⊥DM于点H,利用全等三角形对应边上的高相等,得OG=OH,再由角平分线的判定方法,得MO平分∠AMD,故④正确;若OM平分∠AOD,可得△AMO≌△DMO,进而OA=OC,与已知条件中的OA＜OC矛盾，故③错误