《2025年学习质量监测八年级数学上册人教版》

12. 化简求值：$(a + b + 1)(a - b - 1)-(a + b - 1)(-b - a + 1)+2b(-a + b + 1)$,其中$a$,$b满足\vert a + b - 3\vert+(ab + 2)^{2}= 0$.

答案： 解：原式=a²-(b+1)²+(a+b-1)²-2ab+2b²+2b=a²-b²-2b-1+a²+b²+1+2ab-2a-2b-2ab+2b²+2b=2a²+2b²-2a-2b.
∵|a+b-3|+(ab+2)²=0，
∴|a+b-3|=0，且(ab+2)²=0，
∴a+b=3，ab=-2，
∴原式=2(a²+b²)-2(a+b)=2[(a+b)²-2ab]-2(a+b)=2(a+b)²-4ab-2(a+b)=2×3²-4×(-2)-2×3=18+8-6=20.

1. 已知$(x - 5)^{2}+(x - 7)^{2}= 30$,则$(x - 6)^{2}$的值是(B).
A.13
B.14
C.15
D.16

答案： B

2. 若$a - b + c = 5$,$a + b + c = - 3$,则$c^{2}-ab$的值满足(D).
A.$c^{2}-ab\lt0$
B.$c^{2}-ab\leqslant0$
C.$c^{2}-ab\gt0$
D.$c^{2}-ab\geqslant0$

答案： D

3. 已知$a - b = b - c= \frac{3}{5}$,$a^{2}+b^{2}+c^{2}= 1$,则$ab + bc + ca$的值等于-2/25.

答案： 1. 首先，由$a - b=\frac{3}{5}$，$b - c=\frac{3}{5}$，可得：
$a - c=(a - b)+(b - c)=\frac{3}{5}+\frac{3}{5}=\frac{6}{5}$。
2. 然后，根据完全平方公式$(x - y)^{2}=x^{2}-2xy + y^{2}$，则：
$(a - b)^{2}=a^{2}-2ab + b^{2}$，因为$a - b=\frac{3}{5}$，所以$(a - b)^{2}=(\frac{3}{5})^{2}=\frac{9}{25}$，即$a^{2}-2ab + b^{2}=\frac{9}{25}$ ①；
$(b - c)^{2}=b^{2}-2bc + c^{2}$，因为$b - c=\frac{3}{5}$，所以$(b - c)^{2}=(\frac{3}{5})^{2}=\frac{9}{25}$，即$b^{2}-2bc + c^{2}=\frac{9}{25}$ ②；
$(a - c)^{2}=a^{2}-2ca + c^{2}$，因为$a - c=\frac{6}{5}$，所以$(a - c)^{2}=(\frac{6}{5})^{2}=\frac{36}{25}$，即$a^{2}-2ca + c^{2}=\frac{36}{25}$ ③。
3. 接着，将①$+$②$+$③得：
$(a^{2}-2ab + b^{2})+(b^{2}-2bc + c^{2})+(a^{2}-2ca + c^{2})=\frac{9}{25}+\frac{9}{25}+\frac{36}{25}$。
整理得$2(a^{2}+b^{2}+c^{2})-2(ab + bc + ca)=\frac{9 + 9+36}{25}$。
4. 最后，已知$a^{2}+b^{2}+c^{2}=1$，代入上式：
$2×1-2(ab + bc + ca)=\frac{54}{25}$。
即$2-2(ab + bc + ca)=\frac{54}{25}$。
移项可得$-2(ab + bc + ca)=\frac{54}{25}-2$，$-2(ab + bc + ca)=\frac{54 - 50}{25}$，$-2(ab + bc + ca)=\frac{4}{25}$。
两边同时除以$-2$，得$ab + bc + ca=-\frac{2}{25}$。
故$ab + bc + ca$的值等于$-\frac{2}{25}$。

4. 化简$(x + y + 3)(x + y - 3)-(x - y)^{2}$,其结果为4xy-9.

答案： 4xy-9

5. 如图①是一个长为$4a$、宽为$b$的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(图②).
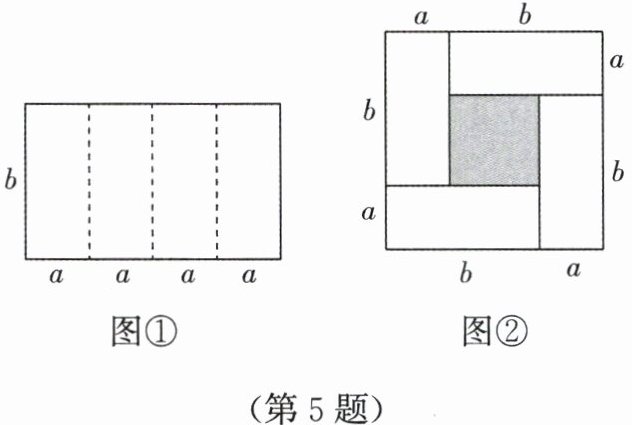
(1)观察图②,写出$(a + b)^{2}$,$(a - b)^{2}$,$ab$之间的等量关系：$(a+b)²-(a-b)²=4ab$.
(2)根据(1)中的结论,若$x + y = 5$,$xy= \frac{9}{4}$,则$x - y= $±4.
(3)拓展应用：若$(2025 - m)^{2}+(m - 2024)^{2}= 15$,求$(2025 - m)(m - 2024)$的值.

答案： 解：
(1)(a+b)²-(a-b)²=4ab
(2)±4
(3)
∵(2025-m)+(m-2024)=1，
∴[(2025-m)+(m-2024)]²=1，
∴(2025-m)²+2(2025-m)(m-2024)+(m-2024)²=1.
∵(2025-m)²+(m-2024)²=15，
∴2(2025-m)(m-2024)=1-15=-14，
∴(2025-m)(m-2024)=-7.