《2025年夺冠百分百新导学课时练八年级数学下册人教版》

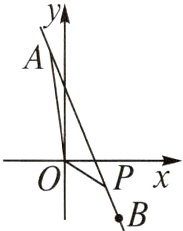
9. (2022雄县期中)如图，直线AB过点A(-1，5)，P(2，a)，B(3，-3).
(1)求直线AB的函数解析式和a的值.
(2)直线AB分别与x轴、y轴交于点C，D，请写出C，D的坐标.
(3)求△AOP的面积.

答案：
解：
(1)设直线$AB$的解析式为$y = kx + b$，将$A(-1,5)$，$B(3,-3)$代入得$\begin{cases}-k + b = 5\\3k + b = -3\end{cases}$，解得$\begin{cases}k = -2\\b = 3\end{cases}$，$\therefore$直线$AB$的解析式为$y = -2x + 3$. 把$P(2,a)$代入$y = -2x + 3$，得$a = -2\times2 + 3 = -1$，$\therefore a$的值是$-1$.
(2)在$y = -2x + 3$中，令$x = 0$得$y = 3$，$\therefore D(0,3)$. 在$y = -2x + 3$中，令$y = 0$得$x = \frac{3}{2}$，$\therefore C(\frac{3}{2},0)$.
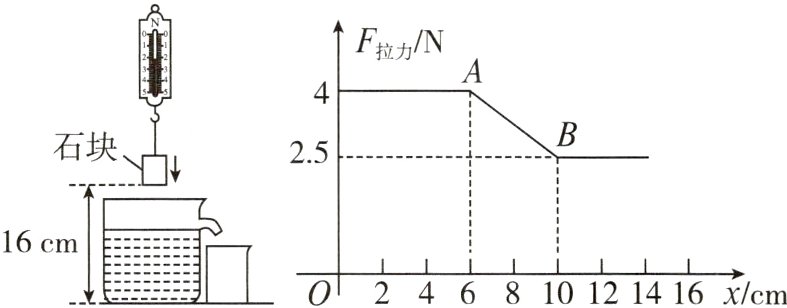
(3)如图， $\because D(0,3)$，$A(-1,5)$，$P(2,-1)$，$\therefore S_{\triangle AOD}=\frac{1}{2}\times3\times1 = \frac{3}{2}$，$S_{\triangle POD}=\frac{1}{2}\times3\times2 = 3$，$\therefore S_{\triangle AOP}=S_{\triangle AOD}+S_{\triangle POD}=\frac{9}{2}$，$\therefore\triangle AOP$的面积为$\frac{9}{2}$.

10. 在测浮力的实验中，将一长方体石块由玻璃器皿的上方，向下缓慢移动浸入水里的过程中，弹簧测力计的示数F拉力(N)与石块下降的高度x(cm)之间的关系如图所示.
(1)求AB所在直线的函数解析式.
(2)当石块下降的高度为8 cm时，求此刻该石块所受浮力的大小.
(温馨提示：当石块位于水面上方时，F拉力=G重力；当石块入水后，F拉力=G重力-F浮力)

答案： 解：
(1)设$AB$所在直线的函数解析式为$F_{拉力}=kx + b$，将$(6,4)$，$(10,2.5)$代入，得$\begin{cases}6k + b = 4\\10k + b = 2.5\end{cases}$，解得$\begin{cases}k = -\frac{3}{8}\\b = \frac{25}{4}\end{cases}$，$\therefore AB$所在直线的函数解析式为$F_{拉力}=-\frac{3}{8}x + \frac{25}{4}$.
(2)在$F_{拉力}=-\frac{3}{8}x + \frac{25}{4}$中，令$x = 8$得$F_{拉力}=-\frac{3}{8}\times8 + \frac{25}{4}=\frac{13}{4}$，$\because 4 - \frac{13}{4}=\frac{3}{4}(N)$，$\therefore$当石块下降的高度为8 cm时，该石块所受浮力为$\frac{3}{4}N$.

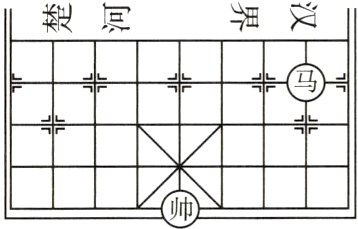
11. (2023鄂州中考)象棋起源于中国，中国象棋文化历史悠久. 如图所示是某次对弈的残图，如果建立平面直角坐标系，使棋子“帅”位于点(-2，-1)的位置，则在同一坐标系下，经过棋子“帅”和“马”所在的点的一次函数解析式为 ( )

A. y=x+1
B. y=x-1
C. y=2x+1
D. y=2x-1

答案： A

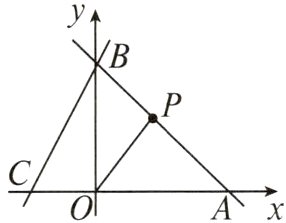
12. (2023遵化期末)如图，直线y=-x+4分别交x轴、y轴于A，B两点，直线BC与x轴交于点C(-2，0)，P是线段AB上的一个动点(点P与A，B不重合).
(1)求直线BC所对应的函数解析式.
(2)设动点P的横坐标为t，△POA的面积为S.
①求出S与t的函数解析式，并写出自变量t的取值范围；
②在线段BC上存在点Q，使得四边形COPQ是平行四边形，求此时点Q的坐标.

答案：
解：
(1)$\because$直线$y = -x + 4$分别交$x$轴、$y$轴于$A$，$B$两点，$\therefore$点$A$的坐标为$(4,0)$，点$B$的坐标为$(0,4)$，设直线$BC$所对应的函数解析式为$y = kx + b$，则$\begin{cases}b = 4\\-2k + b = 0\end{cases}$，解得$\begin{cases}k = 2\\b = 4\end{cases}$，即直线$BC$所对应的函数解析式是$y = 2x + 4$.
(2)①$\because$点$O(0,0)$，点$A(4,0)$，$\therefore OA = 4$，$\because$动点$P$的横坐标为$t$，$\triangle POA$的面积为$S$，$P$是线段$AB$上的一个动点(点$P$与$A$，$B$不重合)，$\therefore$动点$P$的纵坐标为$-t + 4$，$\therefore S=\frac{1}{2}\times4\times(-t + 4)= -2t + 8$，即$S$与$t$的函数解析式是$S = -2t + 8(0 ＜ t ＜ 4)$； ②如图，过点$P$作$PQ// x$轴，交$BC$于点$Q$，$\because$点$P$的坐标为$(t,-t + 4)$，$\therefore$点$Q$的纵坐标为$-t + 4$. $\because$点$Q$在直线$y = 2x + 4$上，$\therefore -t + 4 = 2x + 4$，得$x = -\frac{1}{2}t$. $\because$四边形$COPQ$是平行四边形，$OC = 2$，$\therefore OC = PQ$，$\therefore 2 = t - (-\frac{1}{2}t)$，解得$t = \frac{4}{3}$，$\therefore$点$Q$的坐标为$(-\frac{2}{3},\frac{8}{3})$.