第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 如图,数轴上点$A$所表示的数为$a$,则$a$的值是( )
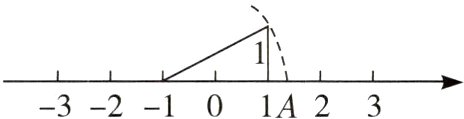
A. $\sqrt{5}+1$
B. $-\sqrt{5}+1$
C. $\sqrt{5}-1$
D. $\sqrt{5}$

A. $\sqrt{5}+1$
B. $-\sqrt{5}+1$
C. $\sqrt{5}-1$
D. $\sqrt{5}$
答案:
C
母题变式
如图,以数轴上的单位长度线段为边作一个正方形,以表示数1的点为圆心、正方形的对角线长为半径画弧,交数轴于点$A$,则点$A$表示的数是( )
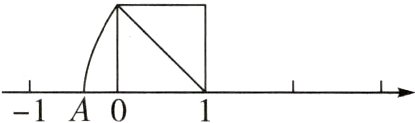
A. $-\sqrt{2}$
B. $1-\sqrt{2}$
C. $-1+\sqrt{2}$
D. $-1-\sqrt{2}$
如图,以数轴上的单位长度线段为边作一个正方形,以表示数1的点为圆心、正方形的对角线长为半径画弧,交数轴于点$A$,则点$A$表示的数是( )

A. $-\sqrt{2}$
B. $1-\sqrt{2}$
C. $-1+\sqrt{2}$
D. $-1-\sqrt{2}$
答案:
B
2. (2023保定雄县期末)如图,在$3\times4$的正方形网格(每个小正方形的边长都是1)中,标记格点$A,B,C,D$,则下列线段长度为$\sqrt{10}$的是( )
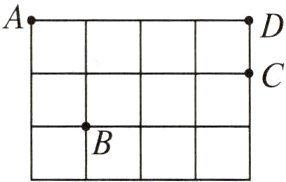
A. 线段$AB$
B. 线段$BC$
C. 线段$AC$
D. 线段$BD$

A. 线段$AB$
B. 线段$BC$
C. 线段$AC$
D. 线段$BD$
答案:
B
3. (2023张家口宣化区期中)图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形$OABC$. 若$AB = BC = 2$,且$\angle AOB = 30^{\circ}$,则$OC$的长度为( )

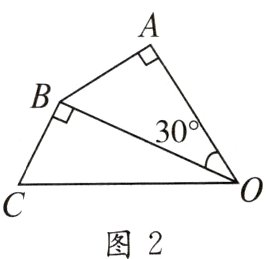
A. $2\sqrt{2}$
B. $2\sqrt{3}$
C. 4
D. $2\sqrt{5}$


A. $2\sqrt{2}$
B. $2\sqrt{3}$
C. 4
D. $2\sqrt{5}$
答案:
D
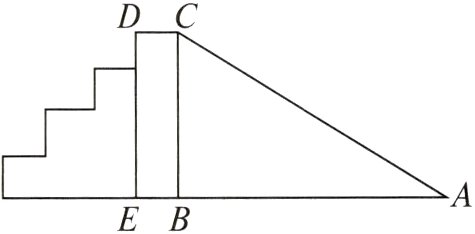
4. (2023保定定州期末)如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道$AC$与$AE$的长度一样,滑梯的高度$BC = 4\ m$,$BE = 1\ m$.则滑道$AC$的长度为________m.

答案:
8.5
5. 在平面直角坐标系中,点$D$的坐标为$(5,0)$,点$P$在第一象限且点$P$的纵坐标为3,当$\triangle ODP$是腰长为5的等腰三角形时,点$P$的坐标为________.
答案:
(1,3)或(4,3)或(9,3)
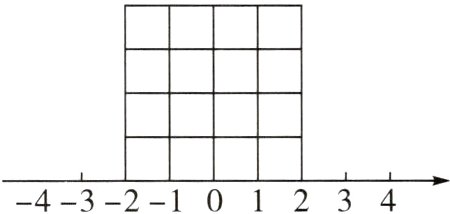
6. 如图,$4\times4$方格纸上每个小正方形的边长都为1.
(1)在方格纸上画一个面积为8的正方形(四个顶点都在格点上).
(2)用圆规在数轴上找出表示$\sqrt{8}$的点(保留作图痕迹).
(1)在方格纸上画一个面积为8的正方形(四个顶点都在格点上).
(2)用圆规在数轴上找出表示$\sqrt{8}$的点(保留作图痕迹).

答案:
解:
(1)如图所示,正方形ABCD的边长为$\sqrt{2^{2}+2^{2}}=2\sqrt{2}$

∴正方形ABCD的面积为$(2\sqrt{2})^{2}=8$,
则正方形ABCD即为所求.
(2)图中的点E是表示$\sqrt{8}$的点.
解:
(1)如图所示,正方形ABCD的边长为$\sqrt{2^{2}+2^{2}}=2\sqrt{2}$

∴正方形ABCD的面积为$(2\sqrt{2})^{2}=8$,
则正方形ABCD即为所求.
(2)图中的点E是表示$\sqrt{8}$的点.
查看更多完整答案,请扫码查看


