《2025年夺冠百分百新导学课时练八年级数学下册人教版》

7. 如图，将长方形分成四个区域，其中$A$，$B$两正方形区域的面积分别是$2$和$18$，则剩余区域的面积是（ ）

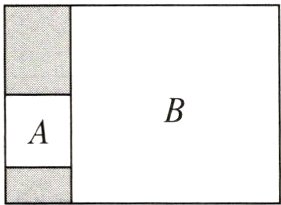
A. $10$
B. $8$
C. $6$
D. $4$

答案： D

8. (2023保定顺平模拟)下列计算中，正确的是（ ）
A. $\sqrt{2}+\sqrt{3}=\sqrt{5}$
B. $3\sqrt{3}-\sqrt{3}=2$
C. $2\sqrt{2}\times3\sqrt{3}=6\sqrt{5}$
D. $\frac{\sqrt{27}+\sqrt{3}}{\sqrt{3}}=4$

答案： D

9. 计算：
(1)$(\sqrt{2}+\sqrt{3})(2\sqrt{2}-\sqrt{3})$.
(2)$(\sqrt{\frac{1}{2}}-2\sqrt{\frac{1}{3}})-(\sqrt{\frac{1}{8}}-\sqrt{75})$.
(3)$(\sqrt{5}-\sqrt{3}+\sqrt{2})(\sqrt{5}-\sqrt{3}-\sqrt{2})$.

答案： 解：
(1)原式 = 1 + $\sqrt{6}$.
(2)原式 = $\frac{1}{4}\sqrt{2}$ + $\frac{13}{3}\sqrt{3}$.
(3)原式 = 6 - 2$\sqrt{15}$.

10. (2022南充仪陇期中)设等式$\sqrt{a(x - a)}+\sqrt{a(y - a)}=\sqrt{x - a}-\sqrt{a - y}$在实数范围内成立，其中$a$，$x$，$y$是两两不同的实数，则$\frac{3x^{2}+xy - y^{2}}{x^{2}-xy + y^{2}}$的值是（ ）
A. $3$
B. $\frac{1}{3}$
C. $2$
D. $\frac{5}{3}$

答案： B

11. (2023衡水景县期末)已知$x = \sqrt{3}+1$，$y = \sqrt{3}-1$，则代数式$x^{2}+2xy + y^{2}$的值为________；代数式$x^{2}-y^{2}$的值为________.

答案： 12 4$\sqrt{3}$

12. 先化简，再求值.
(1)$(a - \sqrt{3})(a + \sqrt{3})-a(a - 6)$，其中$a = \sqrt{5}+\frac{1}{2}$.
(2)$\frac{x^{2}-4x + 4}{x^{3}-2x^{2}}\div(x-\frac{4}{x})$，其中$x = \sqrt{2}-1$.

答案： 解：
(1)原式 = $a^2 - 3 - a^2 + 6a = 6a - 3$，
当 a = $\sqrt{5}$ + $\frac{1}{2}$时，原式 = 6($\sqrt{5}$ + $\frac{1}{2}$) - 3 = 6$\sqrt{5}$.
(2)原式 = $\frac{(x - 2)^2}{x^2(x - 2)}$ ÷ $\frac{x^2 - 4}{x}$ = $\frac{(x - 2)^2}{x^2(x - 2)}$ · $\frac{x}{(x + 2)(x - 2)}$
= $\frac{1}{x(x + 2)}$，
当 x = $\sqrt{2}$ - 1 时，原式 = $\frac{1}{(\sqrt{2} - 1)(\sqrt{2} - 1 + 2)}$ = $\frac{1}{2 - 1}$ = 1.

1. (应用二次根式的性质化简时忽略分类讨论)已知$\vert a\vert = 3$，$\sqrt{b^{2}} = 5$，且$\vert a + b\vert = a + b$，那么$a + b$的值是（ ）
A. $2$或$8$
B. $2$或$-8$
C. $-2$或$8$
D. $-2$或$-8$

答案： A

2. (利用二次根式的性质对式子进行变形时忽略“$-$”号)把$(m - 1)\sqrt{\frac{1}{1 - m}}$中根号前的$(m - 1)$移到根号内得（ ）
A. $\sqrt{m - 1}$
B. $\sqrt{1 - m}$
C. $-\sqrt{m - 1}$
D. $-\sqrt{1 - m}$

答案： D