《2025年夺冠百分百新导学课时练八年级数学下册人教版》

1. 勾股定理：如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么________. 即两直角边的________等于斜边的________.

答案： $a^{2}+b^{2}=c^{2}$ 平方和 平方

2. 勾股定理的验证
勾股定理的验证方法比较多，最常用的方法为拼图法（割补法）.

答案： 面积 之和

1. 在Rt△ABC中，∠C＝90°，∠B＝45°，AB＝1，则AC的长为________.

答案： $\frac{\sqrt{2}}{2}$

2. 在△ABC中，∠A，∠B，∠C所对应的边长分别为a，b，c，∠C＝90°.
（1）若a＝6，b＝8，求c.
（2）若a＝5，c＝13，求b.
（3）若c＝34，a∶b＝8∶15，求a和b.

答案： 解：
(1)在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$\therefore c=\sqrt{a^{2}+b^{2}}=\sqrt{6^{2}+8^{2}}=\sqrt{100}=10$.
(2)在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$\therefore b=\sqrt{c^{2}-a^{2}}=\sqrt{13^{2}-5^{2}}=\sqrt{144}=12$.
(3)$\because a:b = 8:15$，$\therefore$可设$a = 8k$，$b = 15k$，其中$k＞0$. 在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$c = 34$，$\therefore(8k)^{2}+(15k)^{2}=34^{2}$，解得$k = 2$. $\therefore a = 8k = 8\times2 = 16$，$b = 15k = 15\times2 = 30$.

3.（2022保定莲池区校级期末）如图，两个较大正方形的面积分别为576，625，则字母A所代表的正方形的边长为（ ）

A. 1
B. 49
C. 16
D. 7

答案： D

4. 如图，在Rt△ABC中，∠B＝90°，BC＝15，AC＝17，以AB为直径作半圆，则此半圆的面积为________.

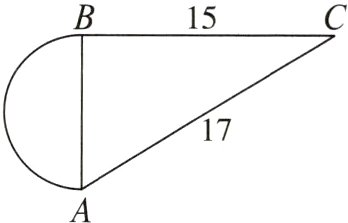
答案： $8\pi$