第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
8. 如图,小巷左、右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7 m,梯子顶端到地面的距离AC为2.4 m. 如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离为1.5 m,则小巷的宽为( )
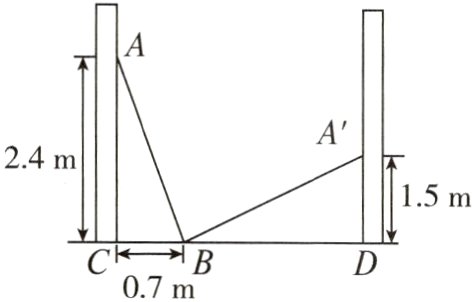
A. 2 m B. 2.5 m
C. 2.6 m D. 2.7 m

A. 2 m B. 2.5 m
C. 2.6 m D. 2.7 m
答案:
D
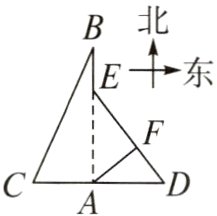
9. 如图,城心公园的著名景点B在大门A的正北方向,游客可以从大门A沿正西方向行至景点C,然后沿笔直的赏花步道到达景点B;也可以从大门A沿正东方向行至景点D,然后沿笔直的临湖步道到达大门A的正北方的景点E,继续沿正北方向行至景点B(点A,B,C,D,E在同一平面内),其中AC=500米,BC=1 300米,AD=600米,BE=400米.
(1)求A,B两点的距离.
(2)为增强游客的游览体验,提升公园品质,将从大门A修建一条笔直的玻璃廊桥AF与临湖步道DE交汇于点F,且玻璃廊桥AF垂直于临湖步道DE,求玻璃廊桥AF的长.
(1)求A,B两点的距离.
(2)为增强游客的游览体验,提升公园品质,将从大门A修建一条笔直的玻璃廊桥AF与临湖步道DE交汇于点F,且玻璃廊桥AF垂直于临湖步道DE,求玻璃廊桥AF的长.

答案:
解:
(1)在Rt△ABC中,∠CAB = 90°,
由勾股定理,得AB = $\sqrt{BC^{2}-AC^{2}}$= $\sqrt{1300^{2}-500^{2}}$= 1 200(米),
∴A,B两点的距离为1 200米.
(2)
∵BE = 400米,AB = 1 200米,
∴AE = 800米.
在Rt△ADE中,∠EAD = 90°,
由勾股定理,得DE = $\sqrt{AE^{2}+AD^{2}}$= $\sqrt{800^{2}+600^{2}}$= 1 000(米),
由面积法,得$\frac{1}{2}$AD·AE = $\frac{1}{2}$DE·AF,
∴AF = $\frac{AD·AE}{DE}$= $\frac{600×800}{1000}$= 480(米),
∴玻璃廊桥AF的长为480米.
(1)在Rt△ABC中,∠CAB = 90°,
由勾股定理,得AB = $\sqrt{BC^{2}-AC^{2}}$= $\sqrt{1300^{2}-500^{2}}$= 1 200(米),
∴A,B两点的距离为1 200米.
(2)
∵BE = 400米,AB = 1 200米,
∴AE = 800米.
在Rt△ADE中,∠EAD = 90°,
由勾股定理,得DE = $\sqrt{AE^{2}+AD^{2}}$= $\sqrt{800^{2}+600^{2}}$= 1 000(米),
由面积法,得$\frac{1}{2}$AD·AE = $\frac{1}{2}$DE·AF,
∴AF = $\frac{AD·AE}{DE}$= $\frac{600×800}{1000}$= 480(米),
∴玻璃廊桥AF的长为480米.
10. (阅读理解题)阅读下列材料,并解答其后的问题:我国古代南宋数学家秦九韶在其所著书《数书九章》中,利用“三斜求积术”十分巧妙地解决了已知三角形三边求其面积的问题,这与西方著名的“海伦公式”是完全等价的. 我们也称这个公式为“海伦 - 秦九韶公式”,该公式是:设在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,△ABC的面积为S=$\frac{\sqrt{(a + b + c)(a + b - c)(a + c - b)(b + c - a)}}{4}$.
(1)【举例应用】已知在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且a=4,b=5,c=7,则△ABC的面积为________.
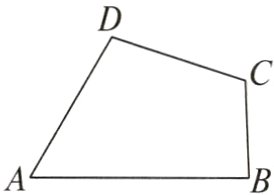
(2)【实际应用】有一块四边形的草地如图所示,现测得AB=(2$\sqrt{6}$+4$\sqrt{2}$)m,BC=5 m,CD=7 m,AD=4$\sqrt{6}$ m,∠A=60°,求这块草地的面积.
(1)【举例应用】已知在△ABC中,∠A,∠B,∠C所对的边分别为a,b,c,且a=4,b=5,c=7,则△ABC的面积为________.
(2)【实际应用】有一块四边形的草地如图所示,现测得AB=(2$\sqrt{6}$+4$\sqrt{2}$)m,BC=5 m,CD=7 m,AD=4$\sqrt{6}$ m,∠A=60°,求这块草地的面积.

答案:
解:
(1)4$\sqrt{6}$
(2)过点D作DE⊥AB,垂足为E,
连接BD,如图.

在Rt△ADE中,
∵∠A = 60°,
∴∠ADE = 30°,
∴AE = $\frac{1}{2}$AD = 2$\sqrt{6}$,
∴BE = AB - AE = 2$\sqrt{6}$+4$\sqrt{2}$-2$\sqrt{6}$= 4$\sqrt{2}$,
DE = $\sqrt{AD^{2}-AE^{2}}$= $\sqrt{(4\sqrt{6})^{2}-(2\sqrt{6})^{2}}$= 6$\sqrt{2}$,
∴BD = $\sqrt{BE^{2}+DE^{2}}$= $\sqrt{(4\sqrt{2})^{2}+(6\sqrt{2})^{2}}$= 2$\sqrt{26}$.
∴S△BCD = 5$\sqrt{10}$,
∵S△ABD = $\frac{1}{2}$AB·DE = $\frac{1}{2}$×(2$\sqrt{6}$+4$\sqrt{2}$)×6$\sqrt{2}$= 12$\sqrt{3}$+24.
∴S四边形ABCD = S△ABD + S△BCD = 12$\sqrt{3}$+24+5$\sqrt{10}$.
答:该块草地的面积为(12$\sqrt{3}$+24+5$\sqrt{10}$)m².
解:
(1)4$\sqrt{6}$
(2)过点D作DE⊥AB,垂足为E,
连接BD,如图.

在Rt△ADE中,
∵∠A = 60°,
∴∠ADE = 30°,
∴AE = $\frac{1}{2}$AD = 2$\sqrt{6}$,
∴BE = AB - AE = 2$\sqrt{6}$+4$\sqrt{2}$-2$\sqrt{6}$= 4$\sqrt{2}$,
DE = $\sqrt{AD^{2}-AE^{2}}$= $\sqrt{(4\sqrt{6})^{2}-(2\sqrt{6})^{2}}$= 6$\sqrt{2}$,
∴BD = $\sqrt{BE^{2}+DE^{2}}$= $\sqrt{(4\sqrt{2})^{2}+(6\sqrt{2})^{2}}$= 2$\sqrt{26}$.
∴S△BCD = 5$\sqrt{10}$,
∵S△ABD = $\frac{1}{2}$AB·DE = $\frac{1}{2}$×(2$\sqrt{6}$+4$\sqrt{2}$)×6$\sqrt{2}$= 12$\sqrt{3}$+24.
∴S四边形ABCD = S△ABD + S△BCD = 12$\sqrt{3}$+24+5$\sqrt{10}$.
答:该块草地的面积为(12$\sqrt{3}$+24+5$\sqrt{10}$)m².
查看更多完整答案,请扫码查看


