《2025年夺冠百分百新导学课时练八年级数学下册人教版》

1. 在下列四组数中，不是勾股数的一组数是（ ）
A. a＝15，b＝8，c＝17
B. a＝9，b＝12，c＝15
C. a＝7，b＝24，c＝25
D. a＝3，b＝4，c＝7

答案： D

2. 在一根长为30个单位的绳子上，依次分别标出A，B，C，D四个点，它们将绳子分成长为5个单位、12个单位和13个单位的三条线段. 自己的一只手握绳子的两个端点（点A和点D），两个同伴分别握住点B和点C，将绳子拉直会得到一个（ ）
A. 直角三角形
B. 锐角三角形
C. 钝角三角形
D. 不能组成三角形

答案： A

3. （2023泸州中考）《九章算术》是中国古代重要的数学著作，该著作中给出了勾股数a，b，c的计算公式：a＝$\frac{1}{2}$（m²－n²），b＝mn，c＝$\frac{1}{2}$（m²＋n²），其中m＞n＞0，m，n是互质的奇数. 下列四组勾股数中，不能由该勾股数计算公式直接得出的是（ ）
A. 3，4，5
B. 5，12，13
C. 6，8，10
D. 7，24，25

答案： C

4. 若8，a，17是一组勾股数，则a＝________.

答案： 15

5. （2022石家庄桥西区校级期末）如图，点A，B，C分别在边长为1的正方形网格顶点上，则∠ABC＝________.

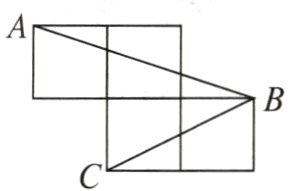
答案： 45°

[母题变式]
如图，在正方形网格中，每一小格的边长为1. P，A，B均为格点.

（1）AP＝________.
（2）点B到直线AP的距离是________.
（3）∠APB＝________.

答案：
(1)$\sqrt{5}$　
(2)$\sqrt{5}$　
(3)135°

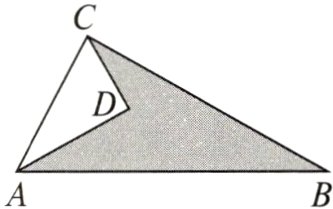
6. （2022石家庄裕华区期末）如图，把一块直角三角形ABC（其中∠ACB＝90°）土地划出一个△ADC后，测得CD＝3米，AD＝4米，BC＝12米，AB＝13米.
（1）根据条件，求AC的长度.
（2）判断△ACD的形状，并说明理由.
（3）求图中阴影部分土地的面积.

答案： 解:
(1)
∵∠ACB=90°,BC=12米,AB=13米,
∴AC = $\sqrt{AB^{2}-BC^{2}}$ = $\sqrt{13^{2}-12^{2}}$ = 5(米).
(2)△ACD是直角三角形
　理由如下:
∵CD=3米,AD=4米,AC=5米,
∴AD²+CD²=AC²=25,
∴∠ADC=90°,
∴△ACD是直角三角形.
(3)$S_{阴影}$ = $S_{\triangle ABC}$ - $S_{\triangle ACD}$ = $\frac{1}{2}$AC·BC - $\frac{1}{2}$AD·CD = $\frac{1}{2}$×5×12 - $\frac{1}{2}$×4×3 = 30 - 6 = 24(平方米).