《2025年夺冠百分百新导学课时练八年级数学下册人教版》

1. 有理数和无理数都可以在数轴上表示出来，即________和数轴上的点是一一对应的.

答案： 实数

2. 平面图形问题从所给的问题中找出或构造________三角形，根据________列式计算.

答案： 直角 勾股定理

3. 立体图形问题是将立体图形转化为______，根据已知条件构造直角三角形，借助勾股定理求斜边长.

答案： 平面图形

1. 将一个长为2，宽为1的长方形$ABCD$按如图方式放在数轴上，使点$A$与原点$O$重合，若以点$O$为圆心，$AC$长为半径画圆，则这个圆与数轴的交点所表示的数是（ ）

A. $\sqrt{5}$
B. $-\sqrt{5}$
C. $\pm\sqrt{5}$
D. $\pm2.5$

答案： C

2. 如图，在正方形网格中，每个小正方形的边长为1，则在网格上的三角形$ABC$中，边长为无理数的边有（ ）

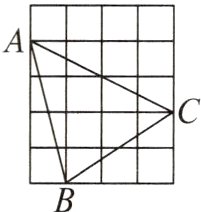
A. 0条
B. 1条
C. 2条
D. 3条

答案： D

3. 如图，在数轴上画出表示$\sqrt{17}$的点.

答案：
解：
(1)在数轴上找出表示4的点B.
(2)过点B作直线l垂直于OB，在直线l上截取BC = 1.
(3)以原点O为圆心，以OC为半径作弧，弧与数轴交于点A.

如图，点A即为所求.

4. (2023黄骅一模)在$Rt\triangle ABC$和$Rt\triangle DEF$中，$\angle C=\angle EFD = 90^{\circ},\angle BAC=\angle E = 30^{\circ}$，$BC = 4$，$DF = 1$，点$F$与点$B$重合，将$\triangle DEF$沿$BA$方向平移，得到$\triangle D'E'F'$，当平移距离为5时，连接$AE'$，则$AE'$的长度为（ ）

A. $\sqrt{3}$
B. $\sqrt{5}$
C. 2
D. $2\sqrt{3}$

答案： D

5. 如图，在$Rt\triangle ABC$中，$AB = 6$，$BC = 4$，$\angle B = 90^{\circ}$，将$\triangle ABC$折叠，使点$A$与$BC$的中点$D$重合，折痕为$MN$，则线段$BN$的长为（ ）

A. $\frac{5}{3}$
B. $\frac{5}{2}$
C. $\frac{8}{3}$
D. 5

答案： C

6. (教材P27练习T2变式)如图，已知等边三角形$ABC$的两个顶点坐标分别为$A(-4,0)$，$B(2,0)$，$CH\perp AB$于点$H$，试求点$C$的坐标和$\triangle ABC$的面积.

答案： 解：
∵A(-4,0)，B(2,0)，
∴OB = 2，AB = 6.
∵△ABC是等边三角形，CH⊥AB，
∴AC = 6，AH = BH = 3，
∴OH = BH - OB = 1.
根据勾股定理，得CH = $\sqrt{AC^{2}-AH^{2}}=3\sqrt{3}$.
∴C(-1,3$\sqrt{3}$)，
$S_{\triangle ABC}=\frac{1}{2}AB\cdot CH=\frac{1}{2}\times6\times3\sqrt{3}=9\sqrt{3}$.