《2025年夺冠百分百新导学课时练八年级数学下册人教版》

7. 制作一个表面积为30 cm²的无盖正方体纸盒，则这个正方体纸盒的棱长是（ ）
A. $\sqrt{6}$ cm
B. $\sqrt{5}$ cm
C. $\sqrt{30}$ cm
D. $\pm\sqrt{5}$ cm

答案： A

8. （教材P3练习T1变式）如图，晓峰收集到一张长方形卡片和一张正方形卡片，它们的面积相等，其中长方形卡片的长为2a，宽为5b，则正方形卡片的边长为________.

答案： $\sqrt{10ab}$

1. （2023保定模拟）若二次根式$\sqrt{x - 1}$有意义，则x的取值范围在数轴上表示正确的是（ ）

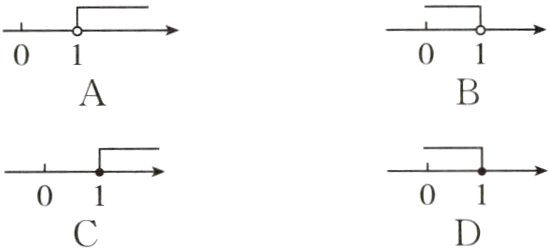
答案： C

2. （2023金华中考）要使$\sqrt{x - 2}$有意义，则x的值可以是（ ）
A. 0
B. -1
C. -2
D. 2

答案： D

母题变式
若$x = 2$能使下列二次根式有意义，则这个二次根式可以是（ ）
A. $\sqrt{x - 3}$
B. $\sqrt{1 - x}$
C. $\sqrt{3 + x}$
D. $\sqrt{-2x}$

答案： C

3. 已知一个正方体的表面积为24 dm²，则这个正方体的棱长为（ ）
A. 1 dm
B. 2 dm
C. $\sqrt{6}$ dm
D. 3 dm

答案： B

4. （陷阱题）如果$\sqrt{x - 2}\cdot\sqrt{x - 3}=0$，那么x的值为________.

答案： 3

5. 若$y = \sqrt{x - 3}+\sqrt{3 - x}-2$，则$\sqrt{x + y}$的值是________.

答案： 1

6. （2022邢台信都区期末）若$\sqrt{300a}$是二次根式，则a的取值范围是__________；若$\sqrt{300a}$是正整数，则正整数a的最小值是________.

答案： $a\geqslant0$　3

7. 求使下列各式有意义的x的取值范围.
（1）$\sqrt{-x^{2}}$.（2）$\sqrt{\frac{2}{x + 1}}$.（3）$\frac{\sqrt{2x + 1}}{2}+\sqrt{3 - x}$.

答案： 解:
(1)当$-x^{2}\geqslant0$,即$x = 0$时,$\sqrt{-x^{2}}$有意义.　
(2)当$x + 1＞0$,即$x＞-1$时,$\sqrt{\frac{2}{x + 1}}$有意义.　
(3)当$2x + 1\geqslant0$且$3 - x\geqslant0$,即$-\frac{1}{2}\leqslant x\leqslant3$时,$\frac{\sqrt{2x + 1}}{2}+\sqrt{3 - x}$有意义.

8. 淇淇想裁剪一块面积为150 cm²的等腰三角形纸片，使它的底边与底边上的高之比为5∶4，则这个三角形的底和高分别是多少？

答案： 解:设三角形的底为$5x$cm，高为$4x$cm，　根据题意，得$\frac{1}{2}\times5x\times4x = 150,x^{2}=15$,　$\because x＞0,\therefore x=\sqrt{15}$　$\therefore$这个三角形的底为$5\sqrt{15}$cm，高为$4\sqrt{15}$cm.

9. 已知a，b分别为等腰三角形的两条边长，且a，b满足$b = 4+\sqrt{3a - 6}+3\sqrt{2 - a}$，求此三角形的周长.

答案： 解:根据二次根式有意义的条件，得$\begin{cases}3a - 6\geqslant0\\2 - a\geqslant0\end{cases}$　解得$a = 2,\therefore b = 4$.　当等腰三角形的三边长为2,2,4时,$2 + 2 = 4$，不符合三角形的三边关系,$\therefore$舍去;当等腰三角形的三边长为2,4,4时，符合三角形的三边关系,$2 + 4 + 4 = 10,\therefore$三角形的周长为10.