《2025年夺冠百分百新导学课时练八年级数学下册人教版》

6.一个小球由静止开始从一个斜坡上向下滚动，滚动的距离s(m)与时间t(s)之间的解析式为s=2t²(t≥0)，通过仪器观察得到小球滚动的距离s(m)与时间t(s)的数据如下表:

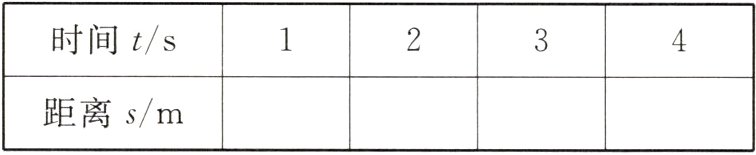
(1)根据解析式完成上表，并画出图象.
(2)当小球滚动6.5 s时，其滚动的距离是多少？

答案： 解：
(1)2 8 18 32 图象略.
(2)当t = 6.5时，s = 84.5，即当小球滚动6.5 s时，其滚动的距离是84.5 m.

7.一个容器有进水管和出水管，每分钟的进水量和出水量是两个常数.从某时刻开始4 min内只进水不出水，从第4 min到第24 min内既进水又出水，从第24 min开始只出水不进水，容器内水量y(L)与时间x(min)之间的关系如图，则图中a的值是 （ ）

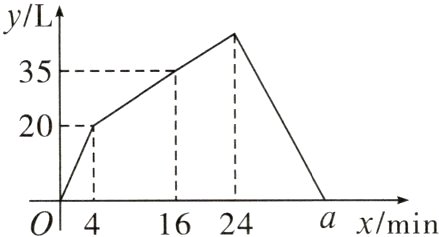
A.32
B.34
C.36
D.38

答案： C

8.某商场为庆祝正式营业，推出了两种购物优惠方案，方案一：非会员购物，所有商品可享九五折优惠；方案二：若支付200元会员费成为该商场会员，则所有商品可享九折优惠.
(1)以x(元)表示商品价格，y(元)表示支出金额，分别写出两种购物方案中y关于x的函数解析式.
(2)若某人计划在该商场购买价格为6 000元的电视机一台，请分析选择哪种方案更省钱.

答案： 解：
(1)方案一：y = 0.95x；
方案二：y = 0.9x + 200.
(2)当x = 6000时，方案一：y = 0.95×6000 = 5700；
方案二：y = 0.9×6000 + 200 = 5600.
∵5700＞5600.
∴选择方案二更省钱.

9.某机动车出发前油箱内有油42 L，行驶若干小时后，在途中加油站加油若干升.油箱中剩余油量Q(L)与行驶时间t(h)之间的函数关系如图，根据图象回答问题：
(1)机动车行驶几小时后加油？加了多少油？
(2)试求加油前油箱剩余油量Q与行驶时间t之间的解析式.
(3)如果加油站离目的地还有230 km，车速为40 km/h，要到达目的地，油箱中的油是否够用？请说明理由.

答案： 解：
(1)由图象知，5小时后加油，加油36 - 12 = 24(L).
(2)观察图象，发现机动车5小时耗油42 - 12 = 30(L)，每小时耗油30÷5 = 6(L)，
∴加油前油箱剩余油量Q与行驶时间t之间的解析式为Q = 42 - 6t.
(3)够用.理由如下：
由图象知，加油后，机动车还能行驶时间：11 - 5 = 6(h)，6×40 = 240(km)，240＞230，故油够用.