第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 如图,在长方形纸片 $ABCD$ 中,$AB = 6$,$AD = 10$,$E$ 为 $CD$ 边上的一点,将 $\triangle ADE$ 沿 $AE$ 翻折,使点 $D$ 恰好落在 $BC$ 边上的点 $F$ 处,则 $BF$ 的长为(

A.$7$
B.$8$
C.$8.6$
D.$9$
B
)
A.$7$
B.$8$
C.$8.6$
D.$9$
答案:
B
2. 如图,将边长为 $8\mathrm{cm}$ 的正方形 $ABCD$ 折叠,使点 $D$ 落在 $BC$ 边的中点 $E$ 处,点 $A$ 落在 $F$ 处,折痕为 $MN$,则线段 $DN$ 的长是

5
。
答案:
5
3. (新考法·数学文化)《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何。”意思是:如图,一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问原处还有多高的竹子。(

A.$4$ 尺
B.$4.55$ 尺
C.$5$ 尺
D.$5.55$ 尺
B
)
A.$4$ 尺
B.$4.55$ 尺
C.$5$ 尺
D.$5.55$ 尺
答案:
B
4. 一辆装满货物,宽为 $2.4\mathrm{m}$ 的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于(

A.$4.1\mathrm{m}$
B.$4.0\mathrm{m}$
C.$3.9\mathrm{m}$
D.$3.8\mathrm{m}$
A
)
A.$4.1\mathrm{m}$
B.$4.0\mathrm{m}$
C.$3.9\mathrm{m}$
D.$3.8\mathrm{m}$
答案:
A
5. 如图,小明准备测量一段水渠的深度,他把一根竹竿 $AB$ 竖直插到水底,此时竹竿 $AB$ 离岸边点 $C$ 处的距离 $CD = 1.5$ 米。竹竿高出水面的部分 $AD$ 长 $0.5$ 米,如果把竹竿的顶端 $A$ 拉向岸边点 $C$ 处,竿顶和岸边的水面刚好相齐,求水渠的深度 $BD$。
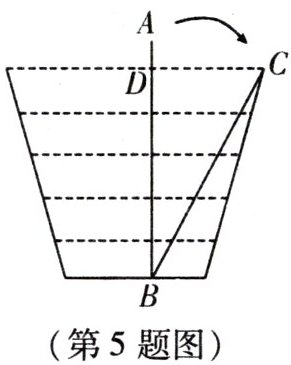

答案:
设水渠深度 $ BD = x $ 米。
因为 $ AD = 0.5 $ 米,所以竹竿总长 $ AB = BD + AD = x + 0.5 $ 米。
当竹竿顶端拉至岸边点 $ C $ 时,竿长不变,即 $ CB = AB = x + 0.5 $ 米。
由题意知 $ CD = 1.5 $ 米,且 $ CD \perp BD $(水平距离与竖直深度垂直),在 $ Rt\triangle CDB $ 中,根据勾股定理:
$ CD^2 + BD^2 = CB^2 $
代入数值:
$ 1.5^2 + x^2 = (x + 0.5)^2 $
化简得:
$ 2.25 + x^2 = x^2 + x + 0.25 $
解得 $ x = 2 $
答:水渠的深度 $ BD $ 为 $ 2 $ 米。
因为 $ AD = 0.5 $ 米,所以竹竿总长 $ AB = BD + AD = x + 0.5 $ 米。
当竹竿顶端拉至岸边点 $ C $ 时,竿长不变,即 $ CB = AB = x + 0.5 $ 米。
由题意知 $ CD = 1.5 $ 米,且 $ CD \perp BD $(水平距离与竖直深度垂直),在 $ Rt\triangle CDB $ 中,根据勾股定理:
$ CD^2 + BD^2 = CB^2 $
代入数值:
$ 1.5^2 + x^2 = (x + 0.5)^2 $
化简得:
$ 2.25 + x^2 = x^2 + x + 0.25 $
解得 $ x = 2 $
答:水渠的深度 $ BD $ 为 $ 2 $ 米。
6. (新考法·跨语文学科)杜甫曾经哀叹“茅屋为秋风所破”,苦于杜甫不曾学过今日几何,不然也不会如此绝望。现在我们来看一茅屋的屋顶剖面(如图),它呈等腰三角形,如果屋檐 $AB = AC = 5\mathrm{m}$,横梁 $BC = 8\mathrm{m}$,那么从梁 $BC$ 上的任意一点 $D$ 要支一根木头顶住屋顶 $A$ 处,这根木头需要的长度可能是(
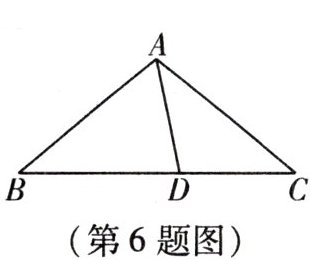
A.$2.5\mathrm{m}$
B.$6\mathrm{m}$
C.$4\mathrm{m}$
D.$8\mathrm{m}$
C
)
A.$2.5\mathrm{m}$
B.$6\mathrm{m}$
C.$4\mathrm{m}$
D.$8\mathrm{m}$
答案:
C
7. 如图,把一张长方形纸片 $ABCD$ 折叠起来,使其顶点 $C$ 与 $A$ 重合,折痕为 $EF$。若 $AB = 1$,$BC = 2$,则 $AF$ 长为

5/4
。
答案:
5/4
查看更多完整答案,请扫码查看


